
【題目】從三角形一個頂點引出一條射線與對邊相交,頂點與交點之間的線段把這個三角形分割成兩個小三角形,如果分得的兩個小三角形中一個為等腰三角形,另一個與原三角形相似,我們把這條線段叫做這個三角形的優美線.
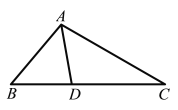
(1)如圖,在△ABC中,AD為角平分線,∠B=50°,∠C=30°,求證:AD為△ABC的優美線;
(2)在△ABC中,∠B=46°,AD是△ABC的優美線,且△ABD是以AB為腰的等腰三角形,求∠BAC的度數.
【答案】(1)見解析;(2)∠BAC的度數為113°.
【解析】
本題是一道新定義圖形的題。
(1)根據三角形的優美線的定義,只要證明△ABD是等腰三角形,△CAD∽△CBA即可解決問題.
(2)如圖2中,分兩種情形討論求解①若AB=AD,△CAD∽△CBA,則∠B=∠ADB=∠CAD,則AC∥BC,這與△ABC這個條件矛盾;②若AB=BD,△CAD∽△CBA.
(1)證明:∵![]() ,
,![]() ,
,
∴![]() .
.
∵AD為角平分線,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴△ABD是等腰三角形.
∵![]() ,
,![]() ,
,
∴△CAD∽△CBA.
∴AD為△ABC的優美線.
(2)∵AD是△ABC的優美線,且△ABD是以AB為腰的等腰三角形,
∴△CAD∽△CBA.
∴![]() .
.
∵△ABD是以AB為腰的等腰三角形,
分兩種情況:
當AB=AD時,
∴![]() .
.
又∵![]() ,
,
∴![]() ,不符合題意,這種情況不存在.
,不符合題意,這種情況不存在.
當AB=BD時,
∴![]() .
.
∴![]() .
.
∴∠BAC的度數為![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,二次函數
中,二次函數![]() 的對稱軸為
的對稱軸為![]() .點
.點![]() 在直線
在直線![]() 上.
上.
(1)求![]() ,
, ![]() 的值;
的值;
(2)若點![]() 在二次函數
在二次函數![]() 上,求
上,求![]() 的值;
的值;
(3)當二次函數![]() 與直線
與直線![]() 相交于兩點時,設左側的交點為
相交于兩點時,設左側的交點為![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
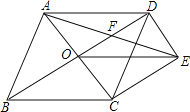
【題目】如圖,菱形ABCD的對角線AC、BD相交于點O,過點D作DE∥AC,且DE=![]() AC,連接CE、OE,連接AE交OD于點F.
AC,連接CE、OE,連接AE交OD于點F.
(1)求證:OE=CD;
(2)若菱形ABCD的邊長為8,∠ABC=60°,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y=﹣![]() ,下列結論:①圖象必經過點(﹣3,1);②圖象在第二,四象限內;③y隨x的增大而增大;④當x>﹣1時,y>3.其中錯誤的結論有( )
,下列結論:①圖象必經過點(﹣3,1);②圖象在第二,四象限內;③y隨x的增大而增大;④當x>﹣1時,y>3.其中錯誤的結論有( )
A. ①④ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于自變量x的不同的取值范圍,有著不同的對應關系,這樣的函數通常叫做分段函數.它是一個函數,而不是幾個函數. 分段函數在自變量x的不同的取值范圍內,函數的表達式也不同.例如:![]() 是分段函數.
是分段函數.
當![]() 時,它是二次函數
時,它是二次函數![]() ;當
;當![]() 時,它是正比例函數
時,它是正比例函數![]() .
.
(1)請在平面直角坐標系中畫出函數![]() 的圖象;
的圖象;
(2)求出y軸左側圖象的最低點的坐標;
(3)當![]() 時,求自變量x的值.
時,求自變量x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=3,AC=4,BC=5,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級兩個班,各選派10名學生參加學校舉行的“漢字聽寫”大賽.各參賽選手成績的數據分析如下表所示,則以下判斷錯誤的是( )
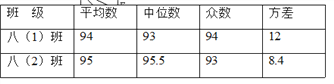
A. 八(2)班的總分高于八(1)班 B. 八(2)班的成績比八(1)班穩定
C. 八(2)班的成績集中在中上游 D. 兩個班的最高分在八(2)班
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點![]() ,
,![]() ,點C是直線AB上異于點B的任一點,現以BC為一邊在AB右側作正方形BCDE,射線OC與直線DE交于點P,若點C的橫坐標為m.
,點C是直線AB上異于點B的任一點,現以BC為一邊在AB右側作正方形BCDE,射線OC與直線DE交于點P,若點C的橫坐標為m.

![]() 求直線AB的函數表達式.
求直線AB的函數表達式.
![]() 若點C在第一象限,且點C為OP的中點,求m的值.
若點C在第一象限,且點C為OP的中點,求m的值.
![]() 若點C為OP的三等分點
若點C為OP的三等分點![]() 即點C分OP成1:2的兩條線段
即點C分OP成1:2的兩條線段![]() ,請直接寫出點C的坐標.
,請直接寫出點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,我們已經學過:點C將線段AB分成兩部分,如果![]() ,那么稱點C為線段AB的黃金分割點.某校的數學拓展性課程班,在進行知識拓展時,張老師由黃金分割點拓展到“黃金分割線”,類似地給出“黃金分割線”的定義:直線l將一個面積為S的圖形分成兩部分,這兩部分的面積分別為S1,S2,如果
,那么稱點C為線段AB的黃金分割點.某校的數學拓展性課程班,在進行知識拓展時,張老師由黃金分割點拓展到“黃金分割線”,類似地給出“黃金分割線”的定義:直線l將一個面積為S的圖形分成兩部分,這兩部分的面積分別為S1,S2,如果![]() ,那么稱直線l為該圖形的黃金分割線.
,那么稱直線l為該圖形的黃金分割線.
如圖2,在△ABC中,∠A=36°,AB=AC,∠C的平分線交AB于點D.
(1)證明點D是AB邊上的黃金分割點;
(2)證明直線CD是△ABC的黃金分割線.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com