
【題目】如圖,在△ABC中,∠C=90°,AC=6cm,BC=8cm,點D從點C出發,以2cm/s的速度沿折線C→A→B向點B運動,同時,點E從點B出發,以1cm/s的速度沿BC邊向點C運動,E到C時兩點同時停止運動。設點E運動的時間為ts(![]() ).
).
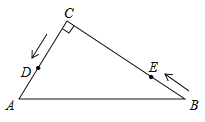
(1)AB=__________cm, CE=__________cm;
(2)當△BDE是直角三角形時,求t的值;
(3)若四邊形CDEF是以CD、DE為一組鄰邊的平行四邊形,
①設平行四邊形CDEF的面積為Scm2,求S于t的關系式;
②是否存在某個時刻t,使□CDEF為菱形?若存在,求出t的值;若不存在,請說明理由.
【答案】(1)10,8-t;(2)![]() 或
或![]() ;(3)①見解析,②存在,
;(3)①見解析,②存在, ![]() .
.
【解析】試題分析:(1)直接利用勾股定理進行求解;
(2)當△BDE是直角三角形時,∠B不可能為直角,所以分兩種情況討論:i)圖1,當∠BED=90°時;ii)圖2,當∠EDB=90°時;利用相似求邊,從而求出t的值;
(3)①根據點D的位置分兩種情況討論:點D在邊AC上時,0<t≤3;點D在邊AB上時,3<t<8;CDEF的面積都等于△CDE面積的二倍;
②當CDEF為菱形,對角線CE和DF互相垂直且平分,利用BH=BE+EH列式計算.
試題解析:(1)由勾股定理得:AB=![]() =10;CE=8-t
=10;CE=8-t
(2)①如圖1,

當∠BED=90°時,△BDE是直角三角形,
則BE=t,AC+AD=2t,
∴BD=6+10-2t=16-2t,
∵∠BED=∠C=90°,
∴DE∥AC,
∴![]() 即
即 ![]()
解得t=![]()
②如圖2,當∠EDB=90°時,△BDE是直角三角形,則BE=t,BD=16-2t,
∴![]() 即
即![]()

解得t=![]()
(3)①如圖3,

當0<t≤3時,BE=t,CD=2t,CE=8-t,
∴S□CDEF=2S△CDE= ![]() =
=![]() =
=![]() ,
,
如圖4,當3<t<8時,BE=t,CE=8-t,過D作DH⊥BC,垂足為H,

∴S□CDEF=2S△CDE= ![]() =
=![]() =
=![]() ;
;
∴S于t的函數關系式為:當0<t≤3時,S=![]() ,當3<t<8時,S=
,當3<t<8時,S=![]() .
.
②存在,如圖5,當□CDEF為菱形時,DH⊥CE,

由CD=DE得:CH=HE,
BH=![]() ,BE=t,EH=
,BE=t,EH=![]()
∴BH=BE+EH,即![]()
解得t=![]() ,
,
即當t=![]() 時,□CDEF為菱形.
時,□CDEF為菱形.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點B出發,沿對角線BD向點D勻速運動,速度為4cm/s,過點P作PQ⊥BD交BC于點Q,以PQ為一邊作正方形PQMN,使得點N落在射線PD上,點O從點D出發,沿DC向點C勻速運動,速度為3cm/s,以O為圓心,0.8cm為半徑作⊙O,點P與點O同時出發,設它們的運動時間為t(單 位:s)(0<t<![]() )。
)。
(1)如圖1,連接DQ平分∠BDC時,t的值為 ;
(2)如圖2,連接CM,若△CMQ是以CQ為底的等腰三角形,求t的值;
(3)請你繼續進行探究,并解答下列問題:
①證明:在運動過程中,點O始終在QM所在直線的左側;
②如圖3,在運動過程中,當QM與⊙O相切時,求t的值;并判斷此時PM與⊙O是否也相切?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,先把一矩形![]() 紙片上下對折,設折痕為
紙片上下對折,設折痕為![]() ;如圖②,再把
;如圖②,再把
點![]() 疊在折痕線
疊在折痕線![]() 上,得到
上,得到![]()
![]() .過
.過![]() 點作
點作![]() ,分別交
,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() .
.
(1)求證: ![]() ∽
∽![]() ;
;
(2)在圖②中,如果沿直線![]() 再次折疊紙片,點
再次折疊紙片,點![]() 能否疊在直線
能否疊在直線![]() 上?請說明理由;
上?請說明理由;
(3)在(2)的條件下,若![]() ,求
,求![]() 的長度.
的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
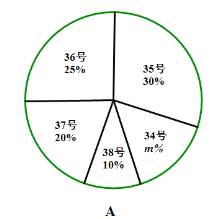
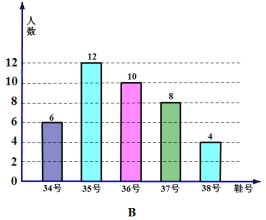
【題目】為了推動陽光體育運動的廣泛開展,引導學生走向操場,走進大自然,走到陽光![]() ,積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用,現從各年的隨機抽取了部分學生的鞋號,繪制了統計圖A和圖B,請根據相關信息,解答下列問題:
,積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用,現從各年的隨機抽取了部分學生的鞋號,繪制了統計圖A和圖B,請根據相關信息,解答下列問題:
(1)本次隨機抽樣的學生數是多少?A中![]() 值是多少?
值是多少?
(2)本次調查獲取的樣本數據的眾數和中位數各是多少?
(3)根據樣本數據,若學校計劃購買200雙運動鞋,建議購買35號運動鞋多少雙?
查看答案和解析>>
科目:初中數學 來源: 題型:
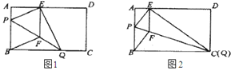
【題目】如圖![]() ,在矩形紙片
,在矩形紙片![]() 中,
中,![]() ,
,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() .過點
.過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() ,
,![]() 也隨之移動.
也隨之移動.
①當點![]() 與點
與點![]() 重合時(如圖
重合時(如圖![]() ),求菱形
),求菱形![]() 的邊長;
的邊長;
②若限定![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上移動,求出點
上移動,求出點![]() 在邊
在邊![]() 上移動的最大距離.
上移動的最大距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,對角線AC,BD相交于點O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求證:四邊形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖已知∠1=∠2,∠BAD=∠BCD,則下列結論:①AB∥CD,②AD∥BC,③∠B=∠D,④∠D=∠ACB,正確的有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,E是AD的中點,延長CE,BA交于點F,連接AC,DF.
(1)求證:四邊形ACDF是平行四邊形;
(2)當CF平分∠BCD時,寫出BC與CD的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△OAB的位置如圖所示.將△OAB繞點O順時針旋轉90°得△OA1B1;再將△OA1B1繞點O順時針旋轉90°得△OA2B2;再將△OA2B2繞點O順時針旋轉90°得△OA3B3;…依此類推,第9次旋轉得到△OA9B9,則頂點A的對應點A9的坐標為_____.
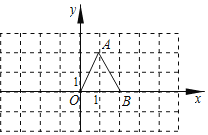
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com