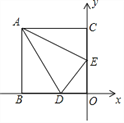
【題目】如圖，矩形ABOC的頂點A的坐標為（-4，5），D是OB的中點，E是OC上的一點，當△ADE的周長最小時，點E的坐標是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】分析: 作A關于y軸的對稱點A′，連接A′D交y軸于E，則此時，△ADE的周長最小，根據A的坐標為（-4，5），得到A′（4，5），B（-4，0），D（-2，0），求出直線DA′的解析式為y=
x+
，即可得到結論．
詳解: 作A關于y軸的對稱點A′,連接A′D交y軸于E，
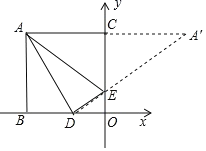
則此時，△ADE的周長最小，
∵四邊形ABOC是矩形，
∴AC∥OB，AC=OB，
∵A的坐標為(4,5)，
∴A′(4,5),B(4,0)，
∵D是OB的中點，
∴D(2,0)，
設直線DA′的解析式為y=kx+b，
∴
，
∴
，
∴直線DA′的解析式為y=x+，
當x=0時,y=，
∴E(0,)，
故選B.
點睛: 此題主要考查軸對稱最短路線問題，解決此類問題，一般都是運用軸對稱的性質，將求折線問題轉化為求線段問題，其說明最短的依據是三角形兩邊之和大于第三邊．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】根據下面給出的數軸，解答下面的問題：
（1）請你根據圖中A、B兩點的位置，分別寫出它們所表示的有理數A： ,B： ；
（2）觀察數軸，與點A的距離為4的點表示的數是： ；
（3）若將數軸折疊，使得A點與﹣3表示的點重合，則B點與數 表示的點重合．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，⊙O的圓心A的坐標為（1，0），半徑為1，點P為直線y=
x+3上的動點，過點P作⊙A的切線，且點為B，則PB的最小值是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
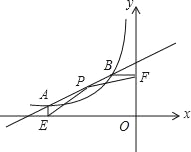
【題目】如圖，函數y=
（x＜0）的圖象與直線y=
x+m相交于點A和點B．過點A作AE⊥x軸于點E，過點B作BF⊥y軸于點F，P為線段AB上的一點，連接PE、PF．若△PAE和△PBF的面積相等，且xP=﹣
，xA﹣xB=﹣3，則k的值是（ ）
A. ﹣5 B. 
C. ﹣2 D. ﹣1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（11分）如圖，四邊形ABCD為菱形，點E為對角線AC上的一個動點，連結DE并延長交AB于點F，連結BE．
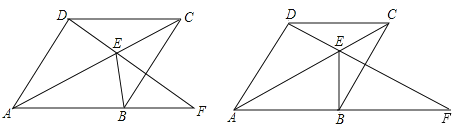
（1）如圖①，求證：∠AFD=∠EBC；
（2）如圖②，若DE=EC且BE⊥AF，求∠DAB的度數；
（3）若∠DAB=90°且當△BEF為等腰三角形時，求∠EFB的度數（只寫出條件與對應的結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
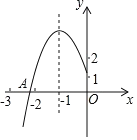
【題目】如圖所示，拋物線
的頂點為D(-1，3)，與
軸的交點A在點(-3，0)和(-2，0)間，以下結論：①
；②
；③
；④
其中正確的有（）個.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校在一次大課間活動中，采用了四鐘活動形式：A、跑步，B、跳繩，C、做操，D、游戲.全校學生都選擇了一種形式參與活動，小杰對同學們選用的活動形式進行了隨機抽樣調查，根據調查統計結果，繪制了不完整的統計圖.
請結合統計圖，回答下列問題：
（1）本次調查學生共 人， 
= ，并將條形圖補充完整；
（2）如果該校有學生2000人，請你估計該校選擇“跑步”這種活動的學生約有多少人？
（3）學校讓每班在A、B、C、D四鐘活動形式中，隨機抽取兩種開展活動，請用樹狀圖或列表的方法，求每班抽取的兩種形式恰好是“跑步”和“跳繩”的概率.
查看答案和解析>>
科目：初中數學 來源： 題型：
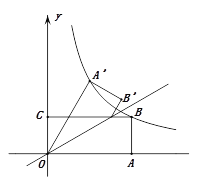
【題目】如圖，矩形OABC的邊OA，OC分別在
軸、
軸上，點B在第一象限，點D在邊BC上，且∠AOD=30°，四邊形OA′B′D與四邊形OABD關于直線OD對稱（點A′和A，B′和B分別對應），若AB=1，反比例函數
的圖象恰好經過點 A′，B，則
的值為_________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點A、D、C、F在同一條直線上，AB=DE，BC=EF，要使△ABC≌△DEF，還需要添加一個條件是（ ）
A. ∠BCA=∠F； B. ∠B=∠E； C. BC∥EF ； D. ∠A=∠EDF
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com