【題目】為了抓住梵凈山文化藝術節的商機，某商店決定購進A、B兩種藝術節紀念品．若購進A種紀念品8件，B種紀念品3件，需要950元；若購進A種紀念品5件，B種紀念品6件，需要800元．
（1）求購進A、B兩種紀念品每件各需多少元？
（2）若該商店決定購進這兩種紀念品共100件，考慮市場需求和資金周轉，用于購買這100件紀念品的資金不少于7500元，但不超過7650元，那么該商店共有幾種進貨方案？
（3）若銷售每件A種紀念品可獲利潤20元，每件B種紀念品可獲利潤30元，在第（2）問的各種進貨方案中，哪一種方案獲利最大？最大利潤是多少元？
【答案】（1）A種紀念品需要100元，購進一件B種紀念品需要50元（2）共有4種進貨方案（3）當購進A種紀念品50件，B種紀念品50件時，可獲最大利潤，最大利潤是2500元
【解析】解：（1）設該商店購進一件A種紀念品需要a元，購進一件B種紀念品需要b元，
根據題意得方程組得：
，…2分
解方程組得：
，
∴購進一件A種紀念品需要100元，購進一件B種紀念品需要50元…4分；
（2）設該商店購進A種紀念品x個，則購進B種紀念品有（100﹣x）個，
∴
，…6分
解得：50≤x≤53，…7分
∵x 為正整數，
∴共有4種進貨方案…8分；
（3）因為B種紀念品利潤較高，故B種數量越多總利潤越高，
因此選擇購A種50件，B種50件．…10分
總利潤=50×20+50×30=2500（元）
∴當購進A種紀念品50件，B種紀念品50件時，可獲最大利潤，最大利潤是2500元．…12分
科目：初中數學 來源： 題型：
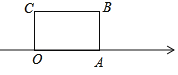
【題目】如圖，面積為30的長方形OABC的邊OA在數軸上，O為原點，OC=5．將長方形OABC沿數軸水平移動，O，A，B，C移動后的對應點分別記為O1， A1， B1， C1，移動后的長方形O1A1B1C1與原長方形OABC重疊部分的面積記為S
（1）當S恰好等于原長方形面積的一半時，數軸上點A1表示的數是多少?
（2）設點A的移動距離AA1=x
①當S=10時，求x的值；
②D為線段AA1的中點，點E在線段OO1上，且OE=
OO1，當點D，E所表示的數互為相反數時，求x的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB∥CD，以點A為圓心，小于AC長為半徑作圓弧，分別交AB，AC于E，F兩點，再分別以E，F為圓心，大于 
EF長為半徑作圓弧，兩條圓弧交于點P，作射線AP，交CD于點M．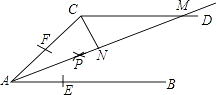 
（1）若∠ACD=114°，求∠MAB的度數；
（2）若CN⊥AM，垂足為N，求證：△ACN≌△MCN．
查看答案和解析>>
科目：初中數學 來源： 題型：
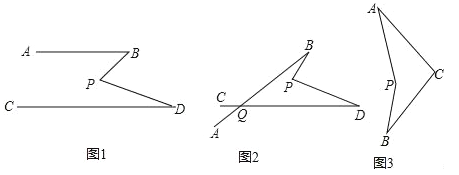
【題目】（1）如圖1，若AB∥CD，將點P在AB、CD內部，∠B，∠D，∠P滿足的數量關系是 ，并說明理由．
（2）在圖1中，將直線AB繞點B逆時針方向旋轉一定角度交直線CD于點Q，如圖2，利用（1）中的結論（可以直接套用），求∠BPD﹑∠B﹑∠D﹑∠BQD之間有何數量關系？
（3）科技活動課上，雨軒同學制作了一個圖（3）的“飛旋鏢”，經測量發現∠PAC＝30°，∠PBC＝35°，他很想知道∠APB與∠ACB的數量關系，你能告訴他嗎？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列各式：
（x﹣1）（x+1）＝x2﹣1；（x﹣1）（x2+x+1）＝x3﹣1；（x﹣1）（x3+x2+x+1）＝x4﹣1．
根據各式的規律，可推測：（x﹣1）（xn﹣1+xn﹣2+…+x+1）＝_____．
根據你的結論計算：1+3+32+33+…+32013+32014的個位數字是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一次函數 y＝kx＋4(k≠0)．
(1)當 x＝－1 時，y＝2，求此函數的表達式；
(2)函數圖象與 x 軸、y 軸的交點分別為 A、B， 求出△AOB 的面積；
(3)利用圖象求出當 y≤3 時，x 的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】列方程解應用題。
端午節期間，某食堂根據職工食用習慣，用700元購進甲、乙兩種粽子260個，其中甲種粽子比乙種粽子少用100元，已知甲種粽子單價比乙種粽子單價高20%，乙種粽子的單價是多少元？甲、乙兩種粽子各購買了多少個？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
