
【題目】如圖,已知線段AB,請按要求完成下列問題.
(1)用直尺和圓規作圖,延長線段AB到點C,使BC=AB;反向延長線段AB到點D,使AD=AC;
(2)如果AB=2cm;
①求CD的長度;
②設點P是線段BD的中點,求線段CP的長度.
![]()
【答案】(1)見解析;(2)①8cm;②5cm.
【解析】
(1)延長線段AB到點C,使BC=AB;反向延長線段AB到點D,使AD=AC,據此作圖即可;
(2)①根據AB=2cm,B是AC的中點,可得AC=2AB=4cm,再根據A是CD的中點,即可得到CD=2AC=8cm;
②根據BD=AD+AB=4+2=6cm,P是線段BD的中點,即可得出BP=3cm,再根據CP=CB+BP進行計算即可.
(1)如圖所示,點C和點D即為所求;
![]()
(2)①∵AB=2cm,B是AC的中點,
∴AC=2AB=4cm,
又∵A是CD的中點,
∴CD=2AC=8cm;
②∵BD=AD+AB=4+2=6cm,P是線段BD的中點,
∴BP=3cm,
∴CP=CB+BP=2+3=5cm.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:
【題目】定義:點C在線段AB上,若BC=![]() AC,則稱點C是線段AB的一個圓周率點.
AC,則稱點C是線段AB的一個圓周率點.
如圖,已知點C是線段AB的一個靠近點A的圓周率點,AC=3.
(1)AB= ;(結果用含![]() 的代數式表示)
的代數式表示)
(2)若點D是線段AB的另一個圓周率點(不同于點C),則CD= ;
(3)若點E在線段AB的延長線上,且點B是線段CE的一個圓周率點.求出BE的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據“算法”的約定:在數值轉換機中,輸入或輸出的值寫在“平行四邊形”框內,計算程序(或步驟)寫在“長方形”框內,菱形框則用于對結果作出是否符合要求的判定.因此畫數值轉換機必須注意框圖的選擇.
(1)如圖,當輸入數字為1時,數值轉換機輸出的結果為 ;
(2)嘉悅的爸爸存入1年期的定期儲蓄10000元(假定1年期定期儲蓄的年利率為4%)到期后本息和(本金和利息的和)自動轉存1年期的定期儲蓄.請畫出數值轉換機,并求出轉存幾次就能使本息和超過11000元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年本市蜜桔大豐收,某水果商銷售一種蜜桔,成本價為10元/千克,已知銷售價不低于成本價,且物價部門規定這種產品的銷售價不高于18元/千克,市場調查發現,該產品每天的銷售量y(千克)與銷售價x(元/千克)之間的函數關系如圖所示:
(1)求y與x之間的函數關系式;
(2)該經銷商想要每天獲得150元的銷售利潤,銷售價應定為多少?
(銷售利潤=銷售價-成本價)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點B(8,0)和點C(9, ![]() ).拋物線
).拋物線![]() (a,c是常數,a≠0)經過點B、C,且與x軸的另一交點為A.對稱軸上有一點M ,滿足MA=MC.
(a,c是常數,a≠0)經過點B、C,且與x軸的另一交點為A.對稱軸上有一點M ,滿足MA=MC.
(1)求這條拋物線的表達式;
(2)求四邊形ABCM的面積;
(3)如果坐標系內有一點D,滿足四邊形ABCD是等腰梯形,且AD//BC,求點D的坐標.
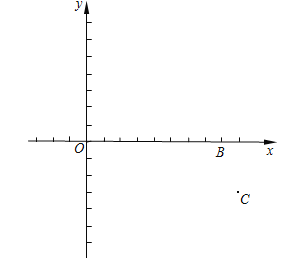
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(﹣2,0),點B的坐標為(0,n),以點B為直角頂點,點C在第二象限內,作等腰直角△ABC.
(1)點C的坐標為 (用字母n表示)
(2)如果△ABC的面積為5.5,求n的值;
(3)在(2)的條件下,坐標平面內是否存在一點M,使以點M、A、B為頂點組成的三角形與△ABC全等?如果存在畫出符合要求的圖形,求出點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級組織知識競賽,共設20道選擇題,各題分值相同,每題必答,如表記錄了5個參賽學生的得分情況,問:
參賽者 | 答對題數 | 答錯題數 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
D | 14 | 6 | 64 |
E | 10 | 10 | 40 |
(1)答對一題得 分,若錯一題得 分;
(2)有一同學說:同學甲得了70分,同學乙得了50分,你認為誰的成績是準確的?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在邊長為1個單位長度的正方形網格中建立如圖所示的平面直角坐標系,△ABC的頂點都在格點上,請解答下列問題:

(1)①作出△ABC向左平移4個單位長度后得到的△A1B1C1, 并寫出點C1的坐標;
②作出△ABC關于原點O對稱的△A2B2C2, 并寫出點C2的坐標;
(2)已知△ABC關于直線l對稱的△A3B3C3的頂點A3的坐標為(-4,-2),請直接寫出直線l的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和頻數分布直方圖的一部分.
請根據圖表信息回答下列問題:
視力 | 頻數(人) | 頻率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次調查的樣本為________,樣本容量為_______;
(2)在頻數分布表中,a=______,b=______,并將頻數分布直方圖補充完整;
(3)若視力在4.6以上(含4.6)均屬正常,根據上述信息估計全區初中畢業生中視力正常的學生有多少人?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com