日本综合视频,亚洲高清在线视频,在线成人亚洲

精英家教網 > 初中數學 > 題目詳情

【題目】平面上，將邊長相等的正三角形、正方形、正五邊形、正六邊形的一邊重合并疊在一起，如圖，則∠3+∠1﹣∠2= ．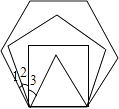

【答案】24°
【解析】解：正三角形的每個內角是：

180°÷3=60°，

正方形的每個內角是：

360°÷4=90°，

正五邊形的每個內角是：

（5﹣2）×180°÷5

=3×180°÷5

=540°÷5

=108°，

正六邊形的每個內角是：

（6﹣2）×180°÷6

=4×180°÷6

=720°÷6

=120°，

則∠3+∠1﹣∠2

=（90°﹣60°）+（120°﹣108°）﹣（108°﹣90°）

=30°+12°﹣18°

=24°．

所以答案是：24°．

【考點精析】掌握多邊形內角與外角和正多邊形和圓是解答本題的根本，需要知道多邊形的內角和定理：n邊形的內角和等于（n-2）180°.多邊形的外角和定理：任意多邊形的外角和等于360°；圓的內接四邊形的對角互補，并且任何一個外角都等于它的內對角；圓的外切四邊形的兩組對邊的和相等．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】填空，完成下列說理過程

如圖，點A，O，B在同一條直線上， OD，OE分別平分∠AOC和∠BOC．

（1）求∠DOE的度數；

（2）如果∠COD=65°，求∠AOE的度數.

解：（1）如圖，因為OD是∠AOC的平分線，

所以∠COD =∠AOC．

因為OE是∠BOC 的平分線，

所以 =∠BOC．

所以∠DOE=∠COD+ =（∠AOC+∠BOC）=∠AOB= °．

（2）由（1）可知∠BOE=∠COE = －∠COD= °.

所以∠AOE= －∠BOE = °．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖1，在中，平分，平分．

(1)若，則的度數為______；

(2)若，直線經過點．

①如圖2，若，求的度數(用含的代數式表示)；

②如圖3，若繞點旋轉，分別交線段于點，試問在旋轉過程中的度數是否會發生改變?若不變，求出的度數(用含的代數式表示)，若改變，請說明理由：

③如圖4，繼續旋轉直線，與線段交于點，與的延長線交于點，請直接寫出與的關系(用含的代數式表示)．

查看答案和解析>>

科目：初中數學 來源： 題型：

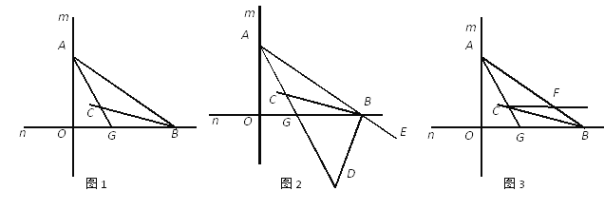
【題目】如圖1，直線m與直線n垂直相交于O，點A在直線m上運動，點B 在直線n上運動，AC、BC分別是∠BAO和∠ABO的角平分線．

（1）求∠ACB的大小；

（2）如圖2，若BD是△AOB的外角∠OBE的角平分線，BD與AC相交于點D，點A、B在運動的過程中，∠ADB的大小是否會發生變化？若發生變化，請說明理由；若不發生變化，試求出其值；

（3）如圖3，過C作直線與AB交于F，且滿足∠AGO－∠BCF=45°，求證：CF∥OB．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，已知矩形ABCD滿足AB：BC=1：，把矩形ABCD對折，使CD與AB重合，得折痕EF，把矩形ABFE繞點B逆時針旋轉90°，得到矩形A′BF′E′，連結E′B，交A′F′于點M，連結AC，交EF于點N，連結AM，MN，若矩形ABCD面積為8，則△AMN的面積為（）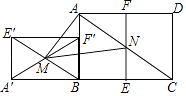

A.4
B.4
C.2
D.1

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】在平面直角坐標系中，△ABC的三個頂點的位置如圖所示，將△ABC水平向左平移3個單位，再豎直向下平移2個單位。

（1）讀出△ABC的三個頂點坐標；

（2）請畫出平移后的△A′B′C′，并直接寫出點A/、B′、C′的坐標；

（3）求平移以后的圖形的面積。

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】已知四邊形ABCD是菱形，在平面直角坐標系中的位置如圖，邊AD經過原點O，已知A（0，﹣3），B（4，0），反比例函數圖象經過點C，直線AC交雙曲線另一支于點E，連接DE，CD，設反比例函數解析式為y1= ，直線AC解析式為y2=ax+b．

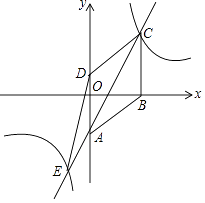
（1）求反比例函數解析式；
（2）當y1＜y2時，求x的取值范圍；
（3）求△CDE的面積．