
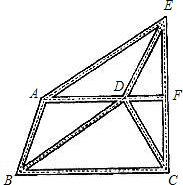
 如圖,是某城市部分街道示意圖,AF∥BC,EC⊥BC,BA∥DE,BD∥AE,甲、乙兩人同時從B站乘車到F站,甲乘1路車,路線是B?A?E?F;乙乘2路車,路線是B?D?C?F,假設兩車速度相同,途中耽誤時間相同,那么誰先到達F站,請說明理由.
如圖,是某城市部分街道示意圖,AF∥BC,EC⊥BC,BA∥DE,BD∥AE,甲、乙兩人同時從B站乘車到F站,甲乘1路車,路線是B?A?E?F;乙乘2路車,路線是B?D?C?F,假設兩車速度相同,途中耽誤時間相同,那么誰先到達F站,請說明理由. 解:可以同時到達.理由如下:
解:可以同時到達.理由如下:

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com