
如圖①,正方形 的頂點
的頂點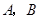 的坐標分別為
的坐標分別為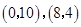 ,頂點
,頂點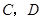 在第一象限.點
在第一象限.點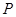 從點
從點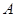 出發,沿正方形按逆時針方向勻速運動,同時,點
出發,沿正方形按逆時針方向勻速運動,同時,點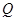 從點
從點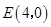 出發,沿
出發,沿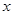 軸正方向以相同速度運動.當點
軸正方向以相同速度運動.當點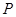 到達點
到達點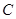 時,
時,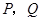 兩點同時停止運動,設運動的時間為
兩點同時停止運動,設運動的時間為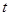 秒.
秒.

(1)求正方形 的邊長.(2分)
的邊長.(2分)
(2)當點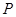 在
在 邊上運動時,
邊上運動時,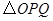 的面積
的面積 (平方單位)與時間
(平方單位)與時間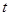 (秒)之間的函數圖象為拋物線的一部分(如圖②所示),求
(秒)之間的函數圖象為拋物線的一部分(如圖②所示),求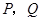 兩點的運動速度.(2分)
兩點的運動速度.(2分)
(3)求(2)中面積 (平方單位)與時間
(平方單位)與時間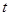 (秒)的函數關系式及面積
(秒)的函數關系式及面積 取最大值時點
取最大值時點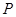 的坐標.(4分)
的坐標.(4分)
(4)若點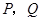 保持(2)中的速度不變,則點
保持(2)中的速度不變,則點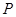 沿著
沿著 邊運動時,
邊運動時,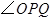 的大小隨著時間
的大小隨著時間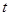 的增大而增大;沿著
的增大而增大;沿著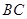 邊運動時,
邊運動時,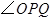 的大小隨著時間
的大小隨著時間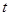 的增大而減小.當點
的增大而減小.當點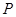 沿著這兩邊運動時,使
沿著這兩邊運動時,使 的點
的點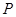 有 個.(2分)
有 個.(2分)
(拋物線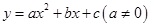 的頂點坐標是
的頂點坐標是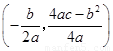 .)
.)
(1)10(2)每秒1個單位(3)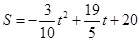 ,
,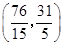 (4)2
(4)2
【解析】(1)作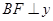 軸于
軸于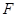 .
.
 ,
,
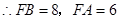 .
.
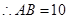 . (2分)
. (2分)
(2)由圖②可知,點 從點
從點 運動到點
運動到點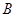 用了10秒.
用了10秒.
又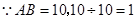 .
.
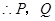 兩點的運動速度均為每秒1個單位. (4分)
兩點的運動速度均為每秒1個單位. (4分)
(3)方法一:作 軸于
軸于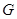 ,則
,則 .
.
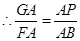 ,即
,即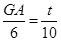 .
.
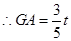 .
.
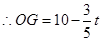 .
.
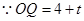 ,
,
 . (6分)
. (6分)
即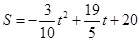 .
.
 ,且
,且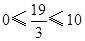 ,
,
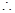 當
當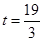 時,
時,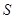 有最大值.
有最大值.
此時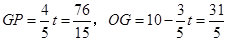 ,
,
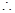 點
點 的坐標為
的坐標為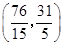 . (8分)
. (8分)
方法二:當 時,
時,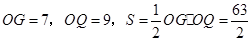 .
.
設所求函數關系式為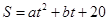 .
.
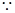 拋物線過點
拋物線過點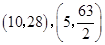 ,
,
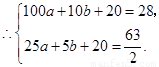

 . (6分)
. (6分)
 ,且
,且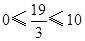 ,
,
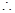 當
當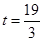 時,
時,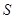 有最大值.
有最大值.
此時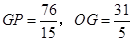 ,
,
 點
點 的坐標為
的坐標為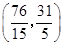 . (8分)
. (8分)
(4)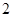 .
.
(1)本題須先作BF⊥y軸于F.再求出FB和FA的值即可得出AB的長.
(2)本題須求出點P從點A運動到點B用了多少時間,再根據AB的長即可求出P、Q兩點的運動速度.
(3)本題須先作PG⊥y軸于G,證出△AGP∽△AFB得出S= 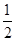 OQ•OG,再把OQ•OG的值代入即可得出
OQ•OG,再把OQ•OG的值代入即可得出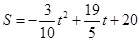 最后即可得出S有最大值時P點的坐標.
最后即可得出S有最大值時P點的坐標.
(4)本題要分兩種情況進行討論:①P在AB上,②P在BC上


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com