【題目】一名大學生利用“互聯網+”自主創業，銷售一種產品，這種產品的成本價為24元/件，已知銷售價不低于成本價，且物價部門規定這種產品的銷售價不高于32元件，市場調查發現，該產品每天的銷售最
（件）與
（元/件）之間的函數關系如圖所示．
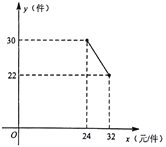
（1）求與之間的函數關系式，并寫出自變量的取值范圍；
（2）求每天的銷售利潤
（元）與銷售單價（元/件）之問的函數關系式并求出每天銷售價為多少元時，每天的銷售利潤最大？最大利潤是多少？
【答案】(1)
與
的函數解析式為
;(2)當銷售價為32元時，每天的銷售利潤最大，最大利潤為176元.
【解析】
(1)根據圖像可以得到與之間的函數關系式是一次函數并且能知道兩個確定的點的坐標，利用待定系數法即可求解出一次函數的解析式，從圖像能得知自變量的取值范圍．
(2)根據題(1)可知產品每天的銷售最（件）與（元/件）之間的函數關系，利用利潤=（售價-成本價）×銷售量，即可列出方程，化簡方程得利潤隨售價的增大而增大，結合自變量的取值范圍即可得到最大利潤．
解：(1)設與的函數解析式為
由題意得：
解得：
∴與的函數解析式為
(2)
∵
，
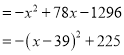
∴當
時，
隨的增大而增大
∴當
時，最大，最大利潤為
元
答：
當銷售價為32元時，每天的銷售利潤最大，最大利潤為176元．
科目：初中數學 來源： 題型：
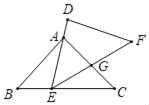
【題目】如圖，在△ABC中，已知，AB＝AC＝6，BC＝10．E是C邊上一動點（E不與點B、C重合），△DEF≌△ABC．其中點A，B的對應點分別是點D、E，且點E在運動時，DE邊始終經過點A，設EF與AC相交于點G，當△AEG為等腰三角形時，則BE的長為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
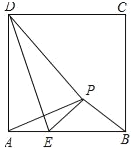
【題目】如圖，正方形ABCD中，AD＝
+2，已知點E是邊AB上的一動點（不與A、B重合）將△ADE沿DE對折，點A的對應點為P，當△APB是等腰三角形時，AE＝_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
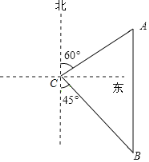
【題目】如圖，一艘輪船從位于燈塔
的北偏東60°方向，距離燈塔60海里的小島
出發，沿正南方向航行一段時間后，到達位于燈塔的南偏東45°方向上的
處，這時輪船與小島的距離是__________海里．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
的正方形網格中，有三個小正方形已經涂成灰色，若再任意涂灰2個白色小正方形（每個白色小正方形被涂成灰色的可能性相同），使新構成灰色部分的圖形是軸對稱圖形的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數y＝ax2+bx+c的部分對應值如表：
利用該二次函數的圖象判斷，當函數值y＞0時，x的取值范圍是（ ）
A.0＜x＜8B.x＜0或x＞8C.﹣2＜x＜4D.x＜﹣2或x＞4
查看答案和解析>>
科目：初中數學 來源： 題型：
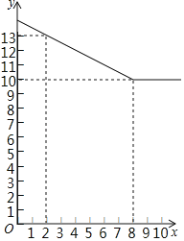
【題目】果農周大爺家的紅心獼猴桃深受廣大顧客的喜愛，獼猴桃成熟上市后，他記錄了10天的銷售數量和銷售單價，其中銷售單價y（元/千克）與時間第x天（x為整數）的數量關系如圖所示，日銷量P（千克）與時間第x天（x為整數）的部分對應值如表所示：
（1）請直接寫出p與x的函數關系式及自變量x的取值范圍；
（2）求y與x的函數關系式，并寫出自變量x的取值范圍；
（3）在這10天中，哪一天銷售額達到最大，最大銷售額是多少元．
查看答案和解析>>
科目：初中數學 來源： 題型：
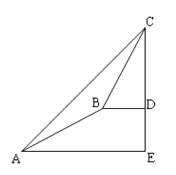
【題目】某數學興趣小組同學進行測量大樹CD高度的綜合實踐活動，如圖，在點A處測得直立于地面的大樹頂端C的仰角為45°，然后沿在同一剖面的斜坡AB行走13米至坡頂B處，然后再沿水平方向行走4米至大樹腳底點D處，斜面AB的坡度（或坡比）i=1：2.4，那么大樹CD的高度為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有七張正面標有數字﹣3，﹣2，﹣1，0，1，2，3的卡片，它們除數字不同外其余全部相同，現將它們背面朝上，洗均后從中隨機抽取一張，記卡片上的數字為a，則使關于x的一元二次方程ax2﹣（2a﹣1）x+a﹣2＝0有兩個不相等的實數根，且分式方程
的解為正數的概率為_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com