
【題目】如圖,在平面直角坐標系中,在平面直角坐標系中,拋物線y=ax2+3x+c與x軸交于A、B兩點,與y軸交于點C(0,8),直線l經過原點O,與拋物線的一個交點為D(6,8).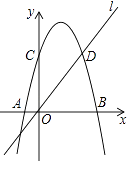
(1)求拋物線的解析式;
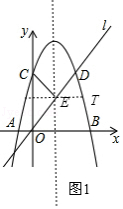
(2)拋物線的對稱軸與直線l交于點E,點T為x軸上方的拋物線上的一個動點.
①當∠TEC=∠TEO時,求點T的坐標;
②直線BT與y軸交于點P,與直線l交于點Q,當OP=OQ時,求點P的坐標.
【答案】
(1)
解:把C、D兩點的坐標代入拋物線解析式可得 ![]() ,解得
,解得 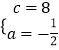 ,
,
∴拋物線解析式為y=﹣ ![]() x2+3x+8
x2+3x+8
(2)
解:①∵y=﹣ ![]() x2+3x+8=﹣
x2+3x+8=﹣ ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
∴拋物線對稱軸為x=3,
設直線l解析式為y=kx,
把D(6,8)代入可得8=6k,解得k= ![]() ,
,
∴直線l的解析式為y= ![]() x,
x,
∴E(3,4),
∵O(0,0),C(0,8),
∴OE=CE,
∴點E在線段OC的垂直平分線上,
∵∠TEC=∠TEO,
∴TE∥x軸,
∴T的縱坐標為4,
在y=﹣ ![]() x2+3x+8中,令y=4可得4=﹣
x2+3x+8中,令y=4可得4=﹣ ![]() x2+3x+8,解得x=3+
x2+3x+8,解得x=3+ ![]() 或x=3﹣
或x=3﹣ ![]() ,
,
∴T的坐標為(3+ ![]() ,4)或(3﹣
,4)或(3﹣ ![]() ,4);
,4);
②在y=﹣ ![]() x2+3x+8中,令y=0可得0=﹣
x2+3x+8中,令y=0可得0=﹣ ![]() x2+3x+8,解得x=﹣2或x=8,
x2+3x+8,解得x=﹣2或x=8,
∴B(8,0),
∵E(3,4),
∴OE=5,
如圖2,過點E作BP的平行線,交y軸于點F,交x軸于點H,
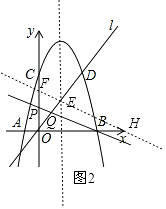
∴ ![]() =
= ![]() ,
,
∵OP=OQ,
∴OF=OE=5,
∴F(0,5),
∴可設直線PB的解析式為y=kx+5,
把E點坐標代入可得4=3k+5,解得k=﹣ ![]() ,
,
∴直線EF的解析式為y=﹣ ![]() x+5,
x+5,
∴可設直線PB的解析式為y=﹣ ![]() x+m,
x+m,
把B點坐標代入可得0=﹣ ![]() ×8+m,解得m=
×8+m,解得m= ![]() ,
,
∴P點坐標為(0, ![]() )
)
【解析】(1)由C、D坐標,利用待定系數法可求得拋物線解析式;(2)①可先求得拋物線的對稱軸和直線l的解析式,則可求得E點坐標,由條件可證得TE∥x軸,則可求得T點縱坐標,代入拋物線解析式,可求得T點坐標;②過E作BP的平行線,交y軸于點F,交x軸于點H,利用平行線分線段成比例可求得OF=OE,可求得F點坐標,則可求得直線EF的解析式,則可設出直線PB的解析式,把B點代入可求得直線PB解析式,可求得P點坐標.


 能力評價系列答案
能力評價系列答案科目:初中數學 來源: 題型:
【題目】為鼓勵居民節約用水,某市對居民用水收費實行“階梯水價”,按每年用水量統計,不超過180立方米的部分按每立方米5元收費;超過180立方米不超過260立方米的部分按每立方米7元收費;超過260立方米的部分按每立方米9元收費.
(1)設每年用水量為x立方米,按“階梯水價”應繳水費y元,請寫出y(元)與x(立方米)之間的函數解析式;
(2)明明家預計2015年全年用水量為200立方米,那么按“階梯水價”收費,她家應繳水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
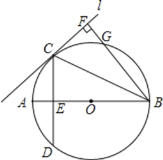
【題目】如圖所示,已知AB是![]() 的直徑,直線L與
的直徑,直線L與![]() 相切于點C,
相切于點C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直線L,垂足為F,BF交
直線L,垂足為F,BF交![]() 于C.
于C.
![]() 圖中哪條線段與AE相等?試證明你的結論;
圖中哪條線段與AE相等?試證明你的結論;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2﹣(2m+1)x+m(m+1)=0
(1)求證:方程總有兩個不相等的實數根;
(2)設方程的兩根分別為x1、x2 , 求x ![]() +x
+x ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一食堂需要購買盒子存放食物,盒子有A、B兩種型號,單個盒子的容量和價格如表格所示.現有15升食物需要存放且要求每個盒子都要裝滿,由于A型號盒子正做促銷活動:購買三個及三個以上可一次性每個返還現金1.5元,則該食堂購買盒子所需的最少費用是 .
型號 | A | B |
單個盒子容量(升) | 2 | 3 |
單價(元) | 5 | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:某商場因換季,將一品牌服裝打折銷售,每件服裝如果按標價的六折出售將虧10元,而按標價的七五折出售將賺50元,問:
(1) 每件服裝的標價是多少元?
(2) 每件服裝的成本是多少元?
(3)為保證不虧本,最多能打幾折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線 ![]() (其中
(其中 ![]() )與x軸交于點A、B(點A在點B的左側),與y軸交于點C,拋物線的對稱軸l與x軸交于點D,且點D恰好在線段BC的垂直平分線上.
)與x軸交于點A、B(點A在點B的左側),與y軸交于點C,拋物線的對稱軸l與x軸交于點D,且點D恰好在線段BC的垂直平分線上.
(1)求拋物線的關系式;
(2)過點 ![]() 的線段MN∥y軸,與BC交于點P,與拋物線交于點N.若點E是直線l上一點,且∠BED=∠MNB-∠ACO時,求點E的坐標.
的線段MN∥y軸,與BC交于點P,與拋物線交于點N.若點E是直線l上一點,且∠BED=∠MNB-∠ACO時,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在銳角△ABC中,∠ABC=45°,高線AD、BE相交于點F.
(1)判斷BF與AC的數量關系并說明理由;
(2)如圖2,將△ACD沿線段AD對折,點C落在BD上的點M,AM與BE相交于點N,當DE∥AM時,判斷NE與AC的數量關系并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com