Question

把兩個全等的等腰Rt△AOB和等腰Rt△DCE（其直角邊長均為4）疊放在一起（如圖1），且使等腰Rt△DCE的直角頂點C與等腰Rt△AOB的斜邊中點C重合．現將等腰Rt△DCE繞C點逆時針方向旋轉（旋轉角a滿足條件：0°＜a＜90°），四邊形CPOQ是旋轉過程中兩三角板的重疊部分（如圖2）．

（1）在圖1中，求點C的坐標為（______，______），點D的坐標為（______，______），點E的坐標為（______，______）；
（2）在上述旋轉過程中，CP與CQ有怎樣的數量關系？四邊形CPOQ的面積有何變化？證明你的結論；
（3）在（2）的前提下，BQ的長度是多少時，△CPQ的面積恰好等于△AOB面積的．

Answer 1

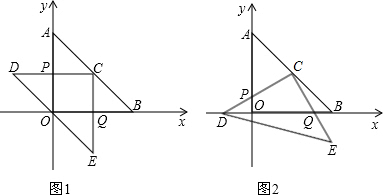
解：（1）由題意知：OA=OB=4，即A（0，4），B（4，0）；
由于C是AB中點，則C（2，2）；
由圖易知：D、C關于y軸對稱，即D（-2，2），同理得：E（2，-2）；
C（2，2）、D（-2，2）、E（2，-2）．

（2）在上述旋轉過程中，CP=CQ，四邊形CPOQ的面積不變，面積為4，是一個定值，
在旋轉過程中其大小始終不變：過點C分別作CM⊥x軸于M點，CN⊥y軸于N點，則CM=CN．
在△CNP與△CMQ中，CM=CN，∠CNP=∠CMQ=90°，
∴∠NCP=∠NCM-∠PCM=90°-∠PCM=∠MCQ，
所以CP=CQ，△CNP與△CMQ的面積相等，
則四邊形CPOQ的面積就是正方形CNOP的面積，
所以四邊形CPOQ的面積=2×2=4．

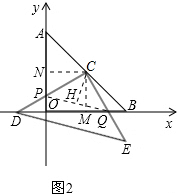
（3）設BQ=a，則MQ=2-a，
在Rt△CMQ中，CQ²=CM²+MQ²=4+（2-a）²，
連接PQ，過C作CH⊥PQ，
∵CP=CQ，∠PCQ=90°，
∴△PCQ為等腰直角三角形，
∴H為PQ中點，
∴CH=HQ，∠CHQ=90°，即△CHQ為等腰直角三角形，
∴CH=HQ=CQ，即CQ=CH=HQ，
∴△CPQ的面積S=PQ•CH=×2×CQ×CQ=CQ²=（4+（2-a）²）=×8，
解得a=1或3，
當BQ=1或3時，△CPQ的面積均等于△AOB的面積的．
分析：（1）已知了等腰直角三角形的直角邊長，即可得到A、B的坐標；由于C是AB的中點，即可求得C點坐標．由圖易知：C、D，C、E分別關于y、x軸對稱，即可得解．
（2）此題要通過構造全等三角形來求解；過C分別作x軸、y軸的垂線，設垂足為M、N；易證得△CPN≌△CQM，即可得CP=CQ，△CPN、△CQM的面積相等，那么四邊形CPOQ的面積，即可轉換為正方形CNOM的面積，由此得解．
（3）設出BQ的長，然后表現出QM的值，即可利用勾股定理求得CQ²的表達式，而△CPQ是等腰直角三角形，那么它的面積為CQ²的一半，根據△AOB的面積可求得△CPQ的面積，即可列出關于BQ長的方程，從而求得BQ的值．
點評：此題主要考查了旋轉的性質、全等三角形的判定和性質以及圖形面積的計算方法，（2）題中，正確地構造出全等三角形是解決此題的關鍵．