Question

求證：在同一底上的兩個角相等的梯形是等腰梯形．
已知：
求證：
證明：

Answer 1

【答案】分析：過D作DE∥AB交BC于E，得出平行四邊形ABED，推出AB=DE，推出∠1=∠B=∠C，推出DE=DC，即可得出答案．
解答：已知：在梯形ABCD中，AD∥BC，∠B=∠C，
求證：AB=DC．
證明：過D作DE∥AB交BC于E，
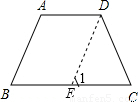
則∠B=∠1，
∵∠B=∠C，
∴∠1=∠C，
∴DE=DC，
∵AD∥BC，AB∥DE，
∴四邊形ABED是平行四邊形，
∴AB=DE．
∴AB=DC．
點評：本題考查了等腰梯形的判定，平行四邊形的性質和判定，等腰三角形的性質和判定的應用，關鍵是能把梯形轉化成平行四邊形和等腰三角形，此題證明方法有多種，如可以延長BA和CD交于O，利用等腰三角形的性質和判定證．