Question

（1）在Rt△ABC中，∠C=90°，∠A的正弦、余弦之間有什么關系？請給出證明過程．
（2）已知銳角α滿足：sinα=1-x，cosα=1-2x，求tanα的值．

Answer 1

解：（1）∵Rt△ABC中，∠C=90°，
∴a²+b²=c²
∵sinA= cosA=
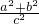
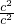
∴sin²A+cos²A=（）²+（）²===1
故sin²A+cos²A=1
（2）由sin²α+cos²α=1，得（1-x）²+（1-2x）²=1，
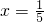
解得或x=1（舍）
∴tanα=====．
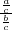
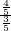
分析：（1）利用正弦與余弦的定義及勾股定理得到同角的正弦與余弦之間的關系；
（2）利用上題證得的關系式代入求解即可．
點評：本題考查了同角的三角函數的關系，解題的關鍵是熟記各個銳角三角函數之間的關系．