
【題目】已知關于x的方程x2+ax+b=0(b≠0)與x2+cx+d=0都有實數根,若這兩個方程有且只有一個公共根,且ab=cd,則稱它們互為“同根輪換方程”.如x2-x-6=0與x2-2x-3=0互為“同根輪換方程”.
(1)若關于x的方程x2+4x+m=0與x2-6x+n=0互為“同根輪換方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分別是方程①和方程②的實數根,且p≠q,b≠0.試問方程①和方程②是否能互為“同根輪換方程”?如果能,用含a的代數式分別表示p和q;如果不能,請說明理由.
b=0,p、q分別是方程①和方程②的實數根,且p≠q,b≠0.試問方程①和方程②是否能互為“同根輪換方程”?如果能,用含a的代數式分別表示p和q;如果不能,請說明理由.
【答案】(1)![]() ;(2)能,①
;(2)能,①![]() ,
,![]() ②
②![]() ,
,![]() ③
③![]() ,
,![]()
【解析】試題分析:(1)根據方程x2+4x+m=0與x2-6x+n=0互為“同根輪換方程”,得到m、n之間的關系為4m=-6n.然后設t是公共根,則有t2+4t+m=0,t2-6t+n=0,于是得到結論;(2)根據x2-x-6=0與x2-2x-3=0互為“同根輪換方程”,得到它們的公共根是3,從而得到當p=q=-3a時,有9a2-3a2+b=0.解得,b=-6a2.解得,p=-3a,x1=2a;q=-3a,x2=a,從而證得方程x2+ax+b=0(b≠0)與x2+2ax+![]() b=0互為“同根輪換方程”.
b=0互為“同根輪換方程”.
試題解析:(1)∵方程x2+4x+m=0與x26x+n=0互為“同根輪換方程”,
∴4m=6n.
設t是公共根,則有t2+4t+m=0,t26t+n=0.
解得,t=![]() .
.
∵4m=6n.∴t=![]() .
.
∴(![]() )2+4(
)2+4(![]() )+m=0.
)+m=0.
∴m=12.
(2)∵x2x6=0與x22x3=0互為“同根輪換方程”,
它們的公共根是3.
而3=(3)×(1)=3×(1).
又∵x2+x6=0與x2+2x3=0互為“同根輪換方程”。
它們的公共根是3.
而3=3×1.
∴當p=q=3a時,
有9a23a2+b=0.
解得:b=6a2.
∴x2+ax6a2=0,x2+2ax3a2=0.
解得:p=3a,x1=2a,q=3a,x2=a.
∵b≠0,
∴6a2≠0,
∴a≠0.
∴2a≠a.即x1≠x2.
又∵2a×![]() b=ab,
b=ab,
∴方程x2+ax+b=0(b≠0)與x2+2ax+12b=0能為“同根輪換方程”,p=q=3a.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:初中數學 來源: 題型:
【題目】列方程求解
(1)m為何值時,關于x的一元一次方程4x﹣2m=3x﹣1的解是x=2x﹣3m的解的2倍.
(2)已知|a﹣3|+(b+1)2=0,代數式![]() 的值比
的值比![]() b﹣a+m多1,求m的值.
b﹣a+m多1,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,BC=4,點P從A點出發,按A→B→C的方向在AB和BC上移動.記PA=x,點D到直線PA的距離為y,則y關于x的函數關系的大致圖像是( )
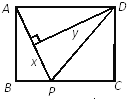
A.  B.
B. 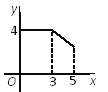 C.
C. 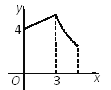 D.
D. 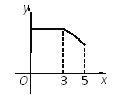
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明早晨跑步,他從自己家出發,向東跑了2km到達小彬家,繼續向東跑了1.5km到達小紅家,然后又向西跑了4.5km到達學校,最后又向東,跑回到自己家.
(1)以小明家為原點,以向東為正方向,用1個單位長度表示1km,在圖中的數軸上,分別用點A表示出小彬家,用點B表示出小紅家,用點C表示出學校的位置;
![]()
(2)求小彬家與學校之間的距離;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多長時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊三角形ABC中,BC=6cm,射線AG∥BC,點E從點A出發沿射線AG以1cm/s的速度運動,點F從點B出發沿射線BC以2cm/s的速度運動.如果點E、F同時出發,設運動時間為t(s)當t=s時,以A、C、E、F為頂點四邊形是平行四邊形. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E、F是ABCD對角線AC上兩點,AE=CF. 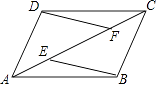
(1)求證:△ABE≌△CDF;
(2)連結DE,BF,求證:四邊形DEBF是平行四邊形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com