
【題目】某班有50位學生,每位學生都有一個序號,將50張編有學生序號(從1號到50號)的卡片(除序號不同外其它均相同)打亂順序重新排列,從中任意抽取1張卡片.
(1)在序號中,是20的倍數的有:20,40,能整除20的有:1,2,4,5,10(為了不重復計數,20只計一次),求取到的卡片上序號是20的倍數或能整除20的概率;
(2)若規定:取到的卡片上序號是k(k是滿足1≤k≤50的整數),則序號是k的倍數或能整除k(不重復計數)的學生能參加某項活動,這一規定是否公平?請說明理由;
(3)請你設計一個規定,能公平地選出10位學生參加某項活動,并說明你的規定是符合要求的.
【答案】
(1)解:∵在序號中,是20的倍數的有:20,40,能整除20的有:1,2,4,5,10(為了不重復計數,20只計一次),
∴是20倍數或者能整除20的數有7個,
則取到的卡片上序號是20的倍數或能整除20的概率為: ![]()
(2)解:不公平;
∵無論k取何值,都能被1整除,則序號為1的學生被抽中的概率為1,即100%,
而很明顯抽到其它序號學生概率不為100%.
∴不公平
(3)解:先抽出一張,記下數字,然后每個數字加5,得到序號,若數字加5超過50,則減掉50,差為序號,直到得到10人為止.
(每個人都有機會)
【解析】(1)由在序號中,是20的倍數的有:20,40,能整除20的有:1,2,4,5,10(為了不重復計數,20只計一次),直接利用概率公式求解即可求得答案;(2)無論k取何值,都能被1整除,則序號為1的學生被抽中的概率為1,即100%,而很明顯抽到其他序號學生概率不為100%.可知此游戲不公平;(3)可設計為:先抽出一張,記下數字,然后每個數字加5,得到序號,若數字加5超過50,則減掉50,差為序號,直到得到10人為止.


 名師指導一卷通系列答案
名師指導一卷通系列答案科目:初中數學 來源: 題型:
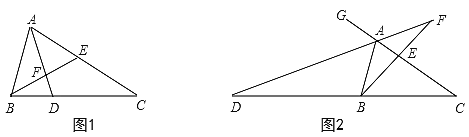
【題目】如圖,在△ABC中,點E在AC上,∠AEB=∠ABC.
(1)圖1中,作∠BAC的角平分線AD,分別交CB、BE于D、F兩點,求證:∠EFD=∠ADC;
(2)圖2中,作△ABC的外角∠BAG的角平分線AD,分別交CB、BE的延長線于D、F兩點,試探究(1)中結論是否仍成立?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
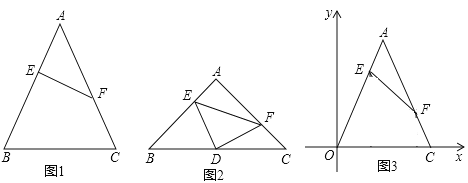
【題目】定義:如圖1,等腰△ABC中,點E,F分別在腰AB,AC上,連結EF,若AE=CF,則稱EF為該等腰三角形的逆等線.
(1)如圖1,EF是等腰△ABC的逆等線,若EF⊥AB,AB=AC=5,AE =2,求逆等線EF的長;
(2)如圖2,若等腰直角△DEF的直角頂點D恰好為等腰直角△ABC底邊BC上的中點,且點E,F分別在AB,AC上,求證:EF為等腰△ABC的逆等線;
(3)如圖3,邊長為6的等邊三角形△AOC的邊OC與X軸重合,EF是該等邊三角形的逆等線.F點的坐標為(5,![]() );試求點E的坐標(若需要,本題可以直接應用結論:在直角三角形中,30°角所對的直角邊等于斜邊的一半.)
);試求點E的坐標(若需要,本題可以直接應用結論:在直角三角形中,30°角所對的直角邊等于斜邊的一半.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖2是裝有三個小輪的手拉車在“爬”樓梯時的側面示意圖,定長的輪架桿OA,OB,OC抽象為線段,有OA=OB=OC,且∠AOB=120°,折線NG﹣GH﹣HE﹣EF表示樓梯,GH,EF是水平線,NG,HE是鉛垂線,半徑相等的小輪子⊙A,⊙B與樓梯兩邊都相切,且AO∥GH. 
(1)如圖2①,若點H在線段OB時,則 ![]() 的值是;
的值是;
(2)如果一級樓梯的高度HE=(8 ![]() +2)cm,點H到線段OB的距離d滿足條件d≤3cm,那么小輪子半徑r的取值范圍是 .
+2)cm,點H到線段OB的距離d滿足條件d≤3cm,那么小輪子半徑r的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校開展“陽光體育”活動,學生會為了解學生最喜歡哪一種球類運動項目,![]() :足球、
:足球、![]() :乒乓球、
:乒乓球、![]() :籃球、
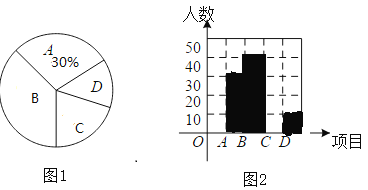
:籃球、![]() :羽毛球,隨機抽取了一部分學生進行調查(要求每位同學只能選擇一種喜歡的球類),并將調查結果繪制成如下兩個不完整的統計圖,如圖1,圖2,請你根據圖中提供的信息解答下列問題。
:羽毛球,隨機抽取了一部分學生進行調查(要求每位同學只能選擇一種喜歡的球類),并將調查結果繪制成如下兩個不完整的統計圖,如圖1,圖2,請你根據圖中提供的信息解答下列問題。
(1)在這次調查中,一共調查了_____名學生;
(2)在圖1扇形統計圖中,求出“![]() ”部分所對應的圓心角等于_____度;
”部分所對應的圓心角等于_____度;
(3)求喜歡籃球的同學占被抽查人數的百分比,并補全頻數分布折線統計圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學習成為商城人的時尚,義烏市新圖書館的啟用,吸引了大批讀者.有關部門統計了2011年10月至2012年3月期間到市圖書館的讀者的職業分布情況,統計圖如下: 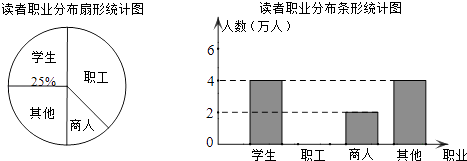
(1)在統計的這段時間內,共有萬人到市圖書館閱讀,其中商人所占百分比是 ,
(2)將條形統計圖補充完整(溫馨提示:作圖時別忘了用0.5毫米及以上的黑色簽字筆涂黑);
(3)若今年4月到市圖書館的讀者共28000名,估計其中約有多少名職工?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,∠A0B=420,點P為∠A0B內一點,分別作出P點關于OA、OB的對稱點P1,P2,連接P1P2交OA于M,交OB于N,P1P2=15,則△PMN的周長為________,∠MPN ________.
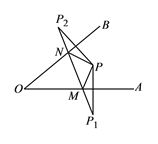
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是邊長為1的正方形ABCD對角線AC上一動點(P與A、C不重合),點E在射線BC上,且PE=PB.設AP=x,△PBE的面積為y.則能夠正確反映y與x之間的函數關系的圖象是( )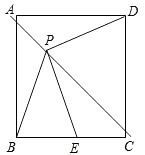
A.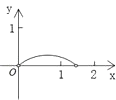
B.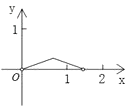
C.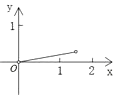
D.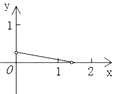
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com