
【題目】某公司推出一款新產品,通過市場調研后,按三種顏色受歡迎的程度分別對A顏色、B顏色、C顏色的產品在成本的基礎上分別加價40%,50%,60%出售(三種顏色產品的成本一樣),經過一個季度的經營后,發現C顏色產品的銷量占總銷量的40%,三種顏色產品的總利潤率為51.5%,第二個季度,公司決定對A產品進行升級,升級后A產品的成本提高了25%,其銷量提高了60%,利潤率為原來的兩倍;B產品的銷量提高到與升級后的A產品的銷量一樣,C產品的銷量比第一季度提高了50%,則第二個季度的總利潤率為_____.
【答案】64% .
【解析】
利潤率=![]() ,單個產品利潤=成本×利潤率,總利潤=成本×利潤率×銷售量.題目沒有給出三種產品明確的成本量和銷售量,故可設原成本為a,A、B、C三種產品原銷售量分別為x、y、z.根據“三種顏色產品的總利潤率為51.5%”得等量關系:A產品利潤+B產品利潤+C產品利潤=總產品利潤;根據“C顏色產品的銷量占總銷量的40%”得等量關系40%×總銷售量=z.用代入消元法整理方程組,得到用z分別表示x和y的式子.第二季度時,根據題意用a、x、z表示各產品的成本、銷售量、利潤率,求三種產品的利潤和和成本和,相除即得到總利潤率.
,單個產品利潤=成本×利潤率,總利潤=成本×利潤率×銷售量.題目沒有給出三種產品明確的成本量和銷售量,故可設原成本為a,A、B、C三種產品原銷售量分別為x、y、z.根據“三種顏色產品的總利潤率為51.5%”得等量關系:A產品利潤+B產品利潤+C產品利潤=總產品利潤;根據“C顏色產品的銷量占總銷量的40%”得等量關系40%×總銷售量=z.用代入消元法整理方程組,得到用z分別表示x和y的式子.第二季度時,根據題意用a、x、z表示各產品的成本、銷售量、利潤率,求三種產品的利潤和和成本和,相除即得到總利潤率.
解:依題意得:三種產品原利潤率分別為40%,50%,60%
設三種顏色產品原來的成本為a,A產品原銷量為x,B產品原銷量為y,C產品原銷量為z,得:
![]()
由②得:x+y=![]() z③
z③
把③代入①整理得:x=![]() z,y=
z,y=![]() z
z
第二季度時,A產品成本為:(1+25%)a=![]() a,B、C產品成本仍為a
a,B、C產品成本仍為a
A、B產品銷售量為:(1+60%)x=![]() x,C產品銷售量為:(1+50%)z=
x,C產品銷售量為:(1+50%)z=![]() z
z
A產品利潤率變為80%,B、C產品利潤率不變
∴總利潤為:![]()
總成本為:![]()
∴總利潤率為: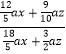 =
=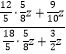 =
=![]() =64%
=64%
故答案為:64%


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點P(x,y),若點Q的坐標為(x,|x﹣y|),則稱點Q為點P的“關聯點”.
(1)請直接寫出點(2,2)的“關聯點”的坐標;
(2)如果點P在函數y=x﹣1的圖象上,其“關聯點”Q與點P重合,求點P的坐標;
(3)如果點M(m,n)的“關聯點”N在函數y=x2的圖象上,當0≤m≤2時,求線段MN的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
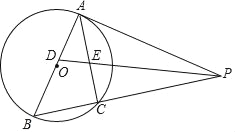
【題目】如圖,以AB為直徑的⊙O外接于△ABC,過A點的切線AP與BC的延長線交于點P,∠APB的平分線分別交AB,AC于點D,E,其中AE,BD(AE<BD)的長是一元二次方程x2﹣5x+6=0的兩個實數根.
(1)求證:PABD=PBAE;
(2)在線段BC上是否存在一點M,使得四邊形ADME是菱形?若存在,請給予證明,并求其面積;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面內由極點、極軸和極徑組成的坐標系叫做極坐標系.如圖,在平面上取定一點O稱為極點;從點O出發引一條射線Ox稱為極軸;線段OP的長度稱為極徑.點P的極坐標就可以用線段OP的長度以及從Ox轉動到OP的角度(規定逆時針方向轉動角度為正)來確定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,則點P關于點O成中心對稱的點Q的極坐標表示不正確的是( )
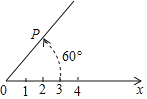
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C在⊙O上,且不與A、B兩點重合,過點C的切線交AB的延長線于點D,連接AC,BC,若∠ABC=53°,則∠D的度數是( )

A. 16°B. 18°C. 26.5°D. 37.5°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列兩則材料,回答問題,
材料一:定義直線y=ax+b與直線y=bx+a互為“互助直線”,例如,直線y=x+4與直y=4x+1互為“互助直線“
材料二:對于平面直角坐標系中的任意兩點P1(x1,y1)、P2(x2,y2),P1、P2兩點間的直角距離d(P1,P2)=|x1﹣x2|+|y1﹣y2|.例如:Q1(﹣3,1)、Q2(2,4)兩點間的直角距離為d(Q1,Q2)=|﹣3﹣2|+|1﹣4|=8
設P0(x0,y0)為一個定點,Q(x,y)是直線y=ax+b上的動點,我們把d(P0,Q)的最小值叫做P0到直線y=ax+b的直角距離.
(1)計算S(﹣1,6),T(﹣2,3)兩點間的直角距離d(S,T)= ,直線y=2x+3上的一點H(a,b)又是它的“互助直線”上的點,求點H的坐標.
(2)對于直線y=ax+b上的任意一點M(m,n),都有點N(3m,2m﹣3n)在它的“互助直線”上,試求點L(5,﹣![]() )到直線y=ax+b的直角距離.
)到直線y=ax+b的直角距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,作直線
,作直線![]() ,將直線
,將直線![]() 下方的二次函數圖象沿直線
下方的二次函數圖象沿直線![]() 向上翻折,與其它剩余部分組成一個組合圖象
向上翻折,與其它剩余部分組成一個組合圖象![]() ,若線段
,若線段![]() 與組合圖象
與組合圖象![]() 有兩個交點,則
有兩個交點,則![]() 的取值范圍為_____.
的取值范圍為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=﹣2x+1與y軸交于點A,與反比例函數y=![]() (k為常數)的圖象有一個交點B的縱坐標是5.
(k為常數)的圖象有一個交點B的縱坐標是5.
(Ⅰ)求反比例函數的解析式,并說明其圖象所在的象限;
(Ⅱ)當2<x<5時,求反比例函數的函數值y的取值范圍;
(Ⅲ)求△AOB的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級為了解學生課堂發言情況,隨機抽取該年級部分學生,對他們某天在課堂上發言的次數進行了統計,其結果如表,并繪制了如圖所示的兩幅不完整的統計圖,已知B、E兩組發言人數的比為5:2,請結合圖中相關數據回答下列問題:
(1)則樣本容量是 ,并補全直方圖;
(2)該年級共有學生500人,請估計全年級在這天里發言次數不少于12的次數;
(3)已知A組發言的學生中恰有1位女生,E組發言的學生中有2位男生,現從A組與E組中分別抽一位學生寫報告,請用列表法或畫樹狀圖的方法,求所抽的兩位學生恰好是一男一女的概率.
發言次數n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com