
【題目】為了解某地區七年級學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,從該地區隨機抽取部分七年級學生作為樣本,采用問卷調查的方法收集數據(參與問卷調查的每名同學只能選擇其中一類節目),并調查得到的數據用下面的表和扇形圖來表示(表、圖都沒制作完成)
節目類型 | 新聞 | 體育 | 動畫 | 娛樂 | 戲曲 |
人數 | 36 | 90 | a | b | 27 |
根據表、圖提供的信息,解決以下問題: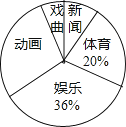
(1)計算出表中a、b的值;
(2)求扇形統計圖中表示“動畫”部分所對應的扇形的圓心角度數;
(3)若該地區七年級學生共有47500人,試估計該地區七年級學生中喜愛“新聞”類電視節目的學生有多少人?
【答案】
(1)
解:∵喜歡體育的人數是90人,占總人數的20%,
∴總人數= ![]() =450(人).
=450(人).
∵娛樂人數占36%,
∴a=450×36%=162(人),
∴b=450﹣162﹣36﹣90﹣27=135(人).
(2)
解:∵喜歡動畫的人數是135人,
∴ ![]() ×360°=108°
×360°=108°
(3)
解:∵喜愛新聞類人數的百分比= ![]() ×100%=8%,
×100%=8%,
∴47500×8%=3800(人).
答:該地區七年級學生中喜愛“新聞”類電視節目的學生有3800人
【解析】(1)先求出抽取的總人數,再求出b的值,進而可得出a的值;
(2)求出a的值與總人數的比可得出結論;
(3)求出喜愛新聞類人數的百分比,進而可得出結論.本題考查的是扇形統計圖,熟知通過扇形統計圖可以很清楚地表示出各部分數量同總數之間的關系.用整個圓的面積表示總數(單位1),用圓的扇形面積表示各部分占總數的百分數是解答此題的關鍵.


科目:初中數學 來源: 題型:
【題目】規定:logab(a>0,a≠1,b>0)表示a,b之間的一種運算.
現有如下的運算法則:lognan=n.logNM= ![]() (a>0,a≠1,N>0,N≠1,M>0).
(a>0,a≠1,N>0,N≠1,M>0).
例如:log223=3,log25= ![]() ,則log1001000=
,則log1001000=
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】郵遞員騎摩托車從郵局出發,先向東騎行2km到達A村,繼續向東騎行3km到達B村,然后向西騎行9km到C村,最后回到郵局.
(1)以郵局為原點,以向東方向為正方向,用1個單位長度表示1km,請你在數軸上表示出A、B、C三個村莊的位置;
![]()
(2)C村離A村有多遠?
(3)若摩托車每1km耗油0.03升,這趟路共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設一次函數y=kx+2k-3(k≠0),對于任意兩個k的值k1,k2,分別對應兩個一次函數值y1,y2,若k1k2<0,當x=m時,取相應y1,y2,中的較小值p,則p的最大值是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列數表

根據數表反映的規律,猜想第6行與第6列的交叉點上的數應為多少.
(1)第n行與第n列的交叉點上的數應為多少.(用含正整數n的式子表示)
(2)計算左上角2×2的正方形里所有數字之和,即:![]()
![]() 在數表中任取幾個2×2的正方形,計算其中所有數字之和,歸納你得出的結論.
在數表中任取幾個2×2的正方形,計算其中所有數字之和,歸納你得出的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b(k<0)與反比例函數y= ![]() 的圖象相交于A、B兩點,一次函數的圖象與y軸相交于點C,已知點A(4,1)
的圖象相交于A、B兩點,一次函數的圖象與y軸相交于點C,已知點A(4,1) 
(1)求反比例函數的解析式;
(2)連接OB(O是坐標原點),若△BOC的面積為3,求該一次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是一塊綠化帶,將陰影部分修建為花圃,已知AB=15,AC=9,BC=12,陰影部分是△ABC的內切圓,一只自由飛翔的小鳥將隨機落在這塊綠化帶上,則小鳥落在花圃上的概率為( ) 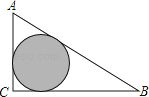
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某市電視臺記者為了解市民獲取新聞的主要圖徑,通過抽樣調查繪制的一個條形統計圖.若該市約有230萬人,則可估計其中將報紙和手機上網作為獲取新聞的主要途徑的總人數大約為萬人.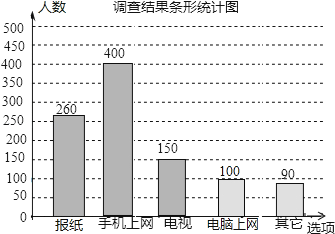
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(6分)下面是小馬虎解的一道題
題目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度數.
解:根據題意可畫出圖,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老師,會判小馬虎滿分嗎?若會,說明理由.若不會,請將小馬虎的的錯誤指出,并給出你認為正確的解法.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com