
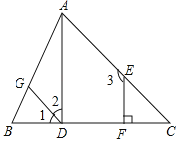
【題目】如圖,已知EF⊥BC,∠1=∠C,∠2+∠3=180°.試說明直線AD與BC垂直.
 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,線段AB=10,動點P從點A出發,以每秒1個單位的速度,沿線段AB向終點B運動,同時,另一個動點Q從點B出發,以每秒3個單位的速度在線段AB上來回運動(從點B向點A運動,到達點A后,立即原速返回,再次到達B點后立即調頭向點A運動.) 當點P到達B點時,P,Q兩點都停止運動.設點P的運動時間為x.

(1)當x=3時,線段PQ的長為 .
(2)當P,Q兩點第一次重合時,求線段BQ的長.
(3)是否存在某一時刻,使點Q恰好落在線段AP的中點上,若存在,請求出所有滿足條件的x的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AG是正八邊形ABCDEFGH的一條對角線.
(1)在剩余的頂點B、C、D、E、F、H中,連接兩個頂點,使連接的線段與AG平行,并說明理由;
(2)兩邊延長AB、CD、EF、GH,使延長線分別交于點P、Q、M、N,若AB=2,求四邊形PQMN的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
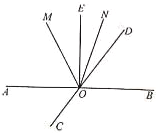
【題目】如圖,直線AB、CD相交于點O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度數;
(2)當∠BOD=x°(0<x<90)時,求∠MON的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,D為 ![]() 的中點,連接OD交弦AC于點F,過點D作DE∥AC,交BA的延長線于點E.
的中點,連接OD交弦AC于點F,過點D作DE∥AC,交BA的延長線于點E. 
(1)求證:DE是⊙O的切線;
(2)連接CD,若OA=AE=4,求四邊形ACDE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰△ABC中,AC=BC,以BC為直徑的⊙O分別與AB,AC相交于點D,E,過點D作DF⊥AC,垂足為點F. 
(1)求證:DF是⊙O的切線;
(2)分別延長CB,FD,相交于點G,∠A=60°,⊙O的半徑為6,求陰影部分的面積. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組研究我國古代《算法統宗》里這樣一首詩:我問開店李三公,眾客都來到店中,一房七客多七客,一房九客一房空.詩中后兩句的意思是:如果每一間客房住7人,那么有7人無房可住;如果每一間客房住9人,那么就空出一間房.
(1)求該店有客房多少間?房客多少人?
(2)假設店主李三公將客房進行改造后,房間數大大增加.每間客房收費20錢,且每間客房最多入住4人,一次性定客房18間以上(含18間),房費按8折優惠.若詩中“眾客”再次一起入住,他們如何訂房更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是正方形ABCD的對角線BD上的一個動點(不與B、D重合),連結AP,過點B作直線AP的垂線,垂足為H,連結DH.若正方形的邊長為4,則線段DH長度的最小值是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣2x+7與x軸、y軸分別相交于點C、B,與直線y=![]() x相交于點A.
x相交于點A.
(1)求A點坐標;
(2)求△OAC的面積;
(3)如果在y軸上存在一點P,使△OAP是以OA為底邊的等腰三角形,求P點坐標;
(4)在直線y=﹣2x+7上是否存在點Q,使△OAQ的面積等于6?若存在,請求出Q點的坐標,若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com