
如圖1,已知菱形ABCD的邊長為2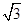 ,點A在x軸負半軸上,點B在坐標原點.點D的坐標為(
,點A在x軸負半軸上,點B在坐標原點.點D的坐標為( ,3),拋物線y=ax2+b(a≠0)經過AB、CD兩邊的中點.
,3),拋物線y=ax2+b(a≠0)經過AB、CD兩邊的中點.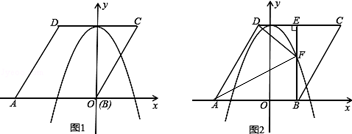
(1)求這條拋物線的函數解析式;
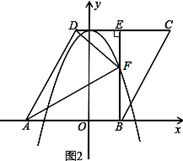
(2)將菱形ABCD以每秒1個單位長度的速度沿x軸正方向勻速平移(如圖2),過點B作BE⊥CD于點E,交拋物線于點F,連接DF、AF.設菱形ABCD平移的時間為t秒(0<t<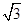 )
)
①當t=1時,△ADF與△DEF是否相似?請說明理由;
②連接FC,以點F為旋轉中心,將△FEC按順時針方向旋轉180°,得△FE′C′,當△FE′C′落在x軸與拋物線在x軸上方的部分圍成的圖形中(包括邊界)時,求t的取值范圍.(寫出答案即可)
(1)y=﹣x2+3
(2)①由對應邊成比例可證得
②畫出旋轉后的圖形,認真分析滿足題意要求時,需要具備什么樣的限制條件,然后根據限制條件列出不等式,求出t的取值范圍.確定限制條件是解題的關鍵
解析試題分析:解:(1)由題意得AB的中點坐標為(﹣ ,0),
,0),
CD的中點坐標為(0,3), 2分
分別代入y=ax2+b得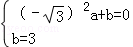 ,解得,
,解得,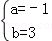 ,
,
∴y=﹣x2+3. 3分
(2)①如圖2所示,在Rt△BCE中,∠BEC=90°,BE=3,BC=2
∴sinC= =
=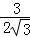 =
=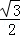 ,∴∠C=60°,∠CBE=30°
,∴∠C=60°,∠CBE=30°
∴EC= BC=
BC=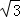 ,DE=
,DE=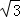 4分
4分
又∵AD∥BC,∴∠ADC+∠C=180°
∴∠ADC=180°﹣60°=120° 5分
∵t=1,
∴B點為(1,0)
∴F(1,2) ,E(1,3)
∴EF=1 6分
在Rt△DEF中
tan∠EDF=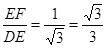
∴∠EDF=300
∴∠ADF=∠ADC—∠EDF=1200—300=900
∴∠ADF=∠DEF
∴DF=2EF=2 7分
又∵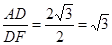 ,
,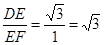
∴
∴△ADF∽△DEF 8分
②如圖3所示,依題意作出旋轉后的三角形△FE′C′,過C′作MN⊥x軸,分別交拋物線、x軸于點M、點N.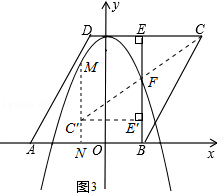
觀察圖形可知,欲使△FE′C′落在指定區域內,必須滿足:EE′≤BE且MN≥C′N.
∵F(t,3﹣t2),∴EF=3﹣(3﹣t2)=t2,∴EE′=2EF=2t2,
由EE′≤BE,得2t2≤3,解得t≤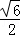 .
.
∵C′E′=CE=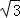 ,∴C′點的橫坐標為t﹣
,∴C′點的橫坐標為t﹣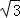 ,
,
∴MN=3﹣(t﹣ )2,又C′N=BE′=BE﹣EE′=3﹣2t2,
)2,又C′N=BE′=BE﹣EE′=3﹣2t2,
由MN≥C′N,得3﹣(t﹣ )2≥3﹣2t2,解得t≥
)2≥3﹣2t2,解得t≥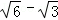 .
.
∴t的取值范圍為: . 11分
. 11分
考點:二次函數、圖形的變換、菱形的性質、三角形相似
點評:本題是中考壓軸題,綜合考查了二次函數的圖象與性質、待定系數法、幾何變換(平移與旋轉)、菱形的性質、相似三角形的判定與性質等重要知識點,難度較大,對考生能力要求很高.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
| 3 |
| 3 |
| 3 |

查看答案和解析>>
科目:初中數學 來源: 題型:
| ||
| 2 |
| a |
| s |
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖1,已知菱形ABCD的邊長為![]() ,點A在x軸負半軸上,點B在坐標原點.點D的坐標為(-
,點A在x軸負半軸上,點B在坐標原點.點D的坐標為(- ![]() ,3),拋物線y=ax2+b(a≠0)經過AB、CD兩邊的中點.
,3),拋物線y=ax2+b(a≠0)經過AB、CD兩邊的中點.
(1)求這條拋物線的函數解析式;
(2)將菱形ABCD以每秒1個單位長度的速度沿x軸正方向勻速平移(如圖2),過點B作BE⊥CD于點E,交拋物線于點F,連接DF、AF.設菱形ABCD平移的時間為t秒(0<t< 3 )
①是否存在這樣的t,使△ADF與△DEF相似?若存在,求出t的值;若不存在,請說明理由;
②連接FC,以點F為旋轉中心,將△FEC按順時針方向旋轉180°,得△FE′C′,當△FE′C′落在x軸與拋物線在x軸上方的部分圍成的圖形中(包括邊界)時,求t的取值范圍.(寫出答案即可)
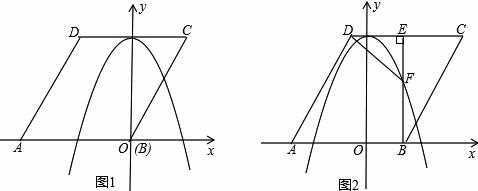
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(浙江臺州卷)數學(帶解析) 題型:解答題
如果三角形有一邊上的中線長恰好等于這邊的長,那么稱這個三角形為“好玩三角形”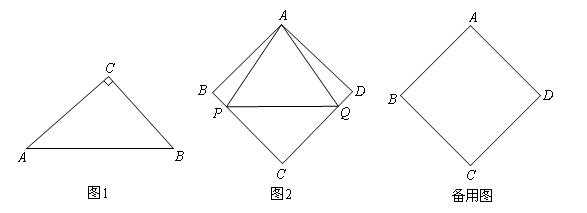
(1)請用直尺與圓規畫一個“好玩三角形”;
(2)如圖1,在Rt△ABC中,∠C=90°,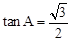 ,求證:△ABC是“好玩三角形”;
,求證:△ABC是“好玩三角形”;
(3)如圖2,已知菱形ABCD的邊長為a, ∠ABC=2β,點P,Q從點A同時出發,以相同的速度分別沿折線AB-BC和AD-DC向終點C運動,記點P所經過的路程為s
①當β=45°時,若△APQ是“好玩三角形”,試求 的值;
的值;
②當tanβ的取值在什么范圍內,點P,Q在運動過程中,有且只有一個△APQ能成為“好玩三角形”?請直接寫出tanβ的取值范圍。
(4)本小題為選做題
依據(3)中的條件,提出一個關于“在點P,Q的運動過程中,tanβ的取值范圍與△APQ是“好玩三角形”的個數關系”的真命題(“好玩三角形”的個數限定不能為1)。
查看答案和解析>>
科目:初中數學 來源:2013年四川省眉山市中考適應性考試數學試卷(解析版) 題型:解答題
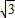 ,點A在x軸負半軸上,點B在坐標原點.點D的坐標為(-
,點A在x軸負半軸上,點B在坐標原點.點D的坐標為(- ,3),拋物線y=ax2+b(a≠0)經過AB、CD兩邊的中點.
,3),拋物線y=ax2+b(a≠0)經過AB、CD兩邊的中點. )
)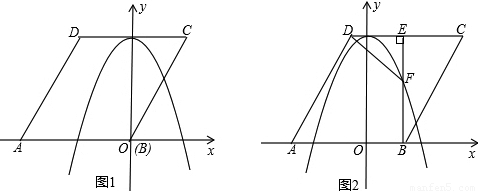
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com