
【題目】已知△ABC,分別以BC,AB,AC為邊作等邊三角形BCE,ACF,ABD
(1)若存在四邊形ADEF,判斷它的形狀,并說明理由.
(2)存在四邊形ADEF的條件下,請你給△ABC添個條件,使得四邊形ADEF成為矩形,并說明理由.
(3)當△ABC滿足什么條件時四邊形ADEF不存在.

【答案】(1)詳見解析;(2)當∠BAC=150°時,四邊形ADEF是矩形;(3)這樣的平行四邊形ADEF不總是存在.
【解析】
(1)根據等邊三角形的性質得出AC=AF,AB=BD,BC=BE,∠EBC=∠ABD=60°,求出∠DBE=∠ABC,根據SAS推出△DBE≌△ABC,根據全等得出DE=AC,求出DE=AF,同理AD=EF,根據平行四邊形的判定推出即可;
(2)當AB=AC時,四邊形ADEF是菱形,根據菱形的判定推出即可;當∠BAC=150°時,四邊形ADEF是矩形,求出∠DAF=90°,根據矩形的判定推出即可;
(3)這樣的平行四邊形ADEF不總是存在,當∠BAC=60°時,此時四邊形ADEF就不存在.
(1)證明:∵△ABD、△BCE和△ACF是等邊三角形,
∴AC=AF,AB=BD,BC=BE,∠EBC=∠ABD=60°,
∴∠DBE=∠ABC=60°﹣∠EBA,
在△DBE和△ABC中
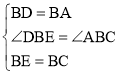 ,
,
∴△DBE≌△ABC,
∴DE=AC,
∵AC=AF,
∴DE=AF,
同理AD=EF,
∴四邊形ADEF是平行四邊形;
(2)解:當∠BAC=150°時,四邊形ADEF是矩形,
理由是:∵△ABD和△ACF是等邊三角形,
∴∠DAB=∠FAC=60°,
∵∠BAC=150°,
∴∠DAF=90°,
∵四邊形ADEF是平行四邊形,
∴四邊形ADEF是矩形;
(3)解:這樣的平行四邊形ADEF不總是存在,
理由是:當∠BAC=60°時,∠DAF=180°,
此時點D、A、F在同一條直線上,此時四邊形ADEF就不存在.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,![]() 是線段
是線段![]() 上一動點,沿
上一動點,沿![]() 以
以![]() 的速度往返運動1次,
的速度往返運動1次,![]() 是線段
是線段![]() 的中點,
的中點,![]() ,設點
,設點![]() 運動時間為
運動時間為![]() 秒
秒![]() .
.
![]()
(1)當![]() 時,求線段
時,求線段![]() 和
和![]() 的長度.
的長度.
(2)用含![]() 的代數式表示運動過程中
的代數式表示運動過程中![]() 的長.
的長.
(3)在運動過程中,若![]() 中點為
中點為![]() ,則
,則![]() 的長是否變化?若不變.求出
的長是否變化?若不變.求出![]() 的長;若發生變化,請說明理由.
的長;若發生變化,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=90°,AD⊥BC,垂足為D.
(1)求作∠ABC的平分線,分別交AD,AC于P,Q兩點;(要求:尺規作圖,保留作圖痕跡,不寫作法)
(2)證明AP=AQ.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,DC=5 cm,在DC上存在一點E,沿直線AE把△AED折疊,使點D恰好落在BC邊上,設落點為F,若△ABF的面積為30 cm2,求△ADE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
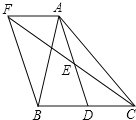
【題目】如圖,在![]() 中,D是BC邊上的一點,E是AD的中點,過A點作BC的平行線交CE的延長線于點F,且
中,D是BC邊上的一點,E是AD的中點,過A點作BC的平行線交CE的延長線于點F,且![]() ,連接BF.
,連接BF.
![]() 證明:
證明:![]() ;
;
![]() 當
當![]() 滿足什么條件時,四邊形AFBD是矩形?并說明理由.
滿足什么條件時,四邊形AFBD是矩形?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富校園文化生活,某校計劃在午間校園廣播臺播放“百家講壇”的部分內容為了了解學生的喜好,抽取若干名學生進行問卷調查(每人只選一項內容),整理調查結果,繪制統計圖如下:
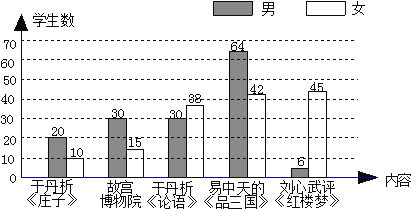
請根據統計圖提供的信息回答以下問題:
(1)這一調查屬于_______(選填“抽樣調查”或“普查”),抽取的學生數為_____名;
(2)估計喜歡收聽易中天《品三國》的學生約占全校學生的____%(精確到小數點后一位);
(3)已知該校女學生共有1800名,則該校喜歡收聽劉心武評《紅樓夢》的女學生大約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個由 5張紙片拼成的平行四邊形,相鄰紙片之間互不重疊也無縫隙,其中兩張等腰直角三角形紙片的面積都為S1 ,另兩張直角三角形紙片的面積都為 S2,中間一張正方形紙片的面積為S3,則這個平行四邊形的面積一定可以表示為( )

A. 4S2B. 4S2+S3C. 3S1+4S3D. 4S1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=90°,AC=AD,M,N分別為AC,CD的中點,連接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )
MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D,則下列說法中正確的個數是( )
①AD是∠BAC的平分線;
②∠ADC=60°;
③點D在AB的中垂線上;
④BD=2CD.

A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com