
【題目】拋物線y=ax2+bx+c(a≠0)與x軸交于點A(﹣1,0),B(4,0),與y軸交于點C(0,2).
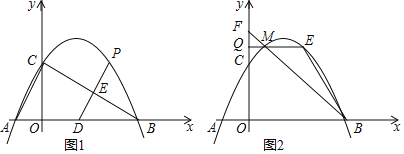
(1)求拋物線的解析式;
(2)如圖1,點D的坐標為(2,0),點P是該拋物線第一象限上的一個動點,連接DP交BC于點E.當△BDE是等腰三角形時,直接寫出此時點E的坐標;
(3)如圖2,點M(m,n)是拋物線上位于對稱軸的左側且不在坐標軸上的動點,過點M作x軸的平行線交y軸于點Q,交拋物線于另一點E,直線BM交y軸于點F,當S△MFQ:S△MEB=1:3時,求出點M的坐標.
【答案】(1)![]() ;(2)點E的坐標為
;(2)點E的坐標為![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ;(3)點M的坐標為
;(3)點M的坐標為![]() ,
,![]() 或
或![]() ,
,![]() .
.
【解析】
(1)根據點![]() ,
,![]() 坐標設成拋物線解析式,再將點
坐標設成拋物線解析式,再將點![]() 坐標代入拋物線解析式中,即可得出結論;
坐標代入拋物線解析式中,即可得出結論;
(2)先判斷出點![]() 在線段
在線段![]() 上,再分三種情況,利用兩點間的距離公式,建立方程求解即可得出結論;
上,再分三種情況,利用兩點間的距離公式,建立方程求解即可得出結論;
(3)先表示出![]() ,求出直線
,求出直線![]() 的解析式,得出點
的解析式,得出點![]() 的坐標,再分三種情況,利用
的坐標,再分三種情況,利用![]() ,建立方程求解,即可得出結論.
,建立方程求解,即可得出結論.
解:(1)![]() 拋物線
拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,
,
![]() 設拋物線的解析式為
設拋物線的解析式為![]() ,
,
![]() 拋物線
拋物線![]() 軸交于點
軸交于點![]() ,
,
![]() ,
,
![]() ,
,
![]() 拋物線的解析式為
拋物線的解析式為![]() ;
;
(2)![]() 點
點![]() 在拋物線第一象限上的一個動點,
在拋物線第一象限上的一個動點,
![]() 點
點![]() 在線段
在線段![]() 上,
上,
![]() ,
,![]() ,
,![]() 直線
直線
![]() 的解析式為
的解析式為![]() ,
,
點![]() 的坐標為
的坐標為![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
![]() 當
當![]() 時,
時,
![]() ,
,
![]()
![]() ,
,
![]() (舍
(舍![]() 或
或![]() ,
,
![]() ,
,![]() ,
,
當![]() 時,
時,
![]() ,
,
![]()
![]() ,
,
![]() 或
或![]() (舍
(舍![]() ,
,
![]() ,
,![]() ,
,
當![]() 時,
時,
![]() 點
點![]() 是
是![]() 的垂直平分線上,
的垂直平分線上,
![]() 點
點![]() 的橫坐標3,
的橫坐標3,
![]() 點
點![]() ,
,
即點![]() 的坐標為
的坐標為![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ;
;
(3)![]() ,
,![]() ,
,
![]() 拋物線的對稱軸直線為
拋物線的對稱軸直線為![]() ,
,
![]() 軸,
軸,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]() ,
,
![]() ,
,
當![]() 時,
時,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() (舍
(舍![]() 或
或![]() ,
,
![]() ,
,![]() ,
,
當![]() 時,
時,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() (舍
(舍![]() 或
或![]() (舍
(舍![]() ,
,
當![]() 時,
時,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() 或
或![]() (舍
(舍![]() ,
,![]() ,
,![]() ,
,
即點![]() 的坐標為
的坐標為![]() ,
,![]() 或
或![]() ,
,![]() ,
,


科目:初中數學 來源: 題型:
【題目】如圖,在3×3正方形方格中,有3個小正方形涂成了黑色,所形成的圖案如圖所示,圖中每塊小正方形除顏色外完全相同.
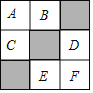
(1)一個小球在這個正方形方格上自由滾動,那么小球停在黑色小正方形的概率是多少?
(2)現將方格內空白的小正方形(A、B、C、D、E、F)中任取2個涂黑,得到新圖案,請用列表或畫樹狀圖的方法求新圖案是中心對稱圖形的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了滿足學生的興趣愛好,學校決定在七年級開設興趣班,興趣班設有四類:![]() 圍棋班;
圍棋班;![]() 象棋班;
象棋班;![]() 書法班;
書法班;![]() 攝影班.為了便于分班,年級組隨機抽查了部分學生的選課意向(每人選報一類),并繪制了如圖所示的兩幅統計圖(不完整),請根據圖中信息,解答下問題:
攝影班.為了便于分班,年級組隨機抽查了部分學生的選課意向(每人選報一類),并繪制了如圖所示的兩幅統計圖(不完整),請根據圖中信息,解答下問題:
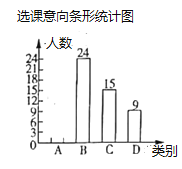
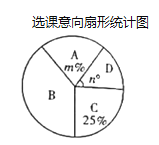
(1)求扇形統計圖中![]() 、
、![]() 的值,并補全條形統計圖;
的值,并補全條形統計圖;
(2)已知該校七年級有600名學生,學校計劃開設三個“圍棋班”,每班要求不超過40人,實行隨機分班.
①學校的開班計劃是否能滿足選擇“圍棋班”的學生意愿,說明理由;
②展鵬、展飛是一對雙胞胎,他們都選擇了“圍棋班”,并且希望能分到同一個班,用樹狀圖或列表法求他們的希望得以實現的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,河旁有一座小山,從山頂A處測得河對岸點C的俯角為30°,測得岸邊點D的俯角為45°,現從山頂A到河對岸點C拉一條筆直的纜繩AC,如果AC是120米,求河寬CD的長?
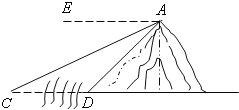
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是雙曲線y=![]() 上的動點,連結AO并延長交雙曲線于點B,將線段AB繞B順時針旋轉60°得到線段BC,點C在雙曲線y=
上的動點,連結AO并延長交雙曲線于點B,將線段AB繞B順時針旋轉60°得到線段BC,點C在雙曲線y=![]() 上的運動,則k=____.
上的運動,則k=____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與反比例函數
,與反比例函數![]() 在第二象限內的圖象相交于點
在第二象限內的圖象相交于點![]() .
.
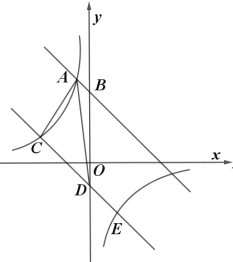
![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 將直線
將直線![]() 向下平移
向下平移![]() 個單位后與反比例函數的圖象交于點
個單位后與反比例函數的圖象交于點![]() 和點
和點![]() 與
與![]() 軸交于點
軸交于點![]() 求
求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,經過
,經過![]() 、
、![]() 兩點的拋物線
兩點的拋物線![]() 與
與![]() 軸的另一交點
軸的另一交點![]() .
.
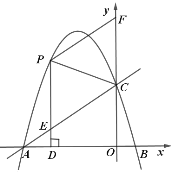
(1)求該拋物線的函數表達式;
(2)![]() 是該拋物線上的動點,過點
是該拋物線上的動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
①求出四邊形![]() 的周長
的周長![]() 與
與![]() 的函數表達式,并求
的函數表達式,并求![]() 的最大值;
的最大值;
②當![]() 為何值時,四邊形
為何值時,四邊形![]() 是菱形;
是菱形;
③是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出滿足條件的點
相似?若存在,請求出滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游樂園有一個直徑為16米的圓形噴水池,噴水池的周邊有一圈噴水頭,噴出的水柱為拋物線,在距水池中心3米處達到最高,高度為5米,且各方向噴出的水柱恰好在噴水池中心的裝飾物處匯合.如圖所示,以水平方向為x軸,噴水池中心為原點建立直角坐標系.
(1)求水柱所在拋物線(第一象限部分)的函數表達式;
(2)王師傅在噴水池內維修設備期間,噴水管意外噴水,為了不被淋濕,身高1.8米的王師傅站立時必須在離水池中心多少米以內?
(3)經檢修評估,游樂園決定對噴水設施做如下設計改進:在噴出水柱的形狀不變的前提下,把水池的直徑擴大到32米,各方向噴出的水柱仍在噴水池中心保留的原裝飾物(高度不變)處匯合,請探究擴建改造后噴水池水柱的最大高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個函數,自變量x取a時,函數值y也等于a,我們稱a為這個函數的不動點.如果二次函數y=x2+2x+c有兩個相異的不動點x1、x2,且x1<1<x2,則c的取值范圍是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com