【題目】如圖，將ABCD沿EF折疊，恰好使點C與點A重合，點D落在點G處，連接AC、CF．
（1）求證：△ABE≌△AGF．
（2）判斷四邊形AECF的形狀，說明理由．
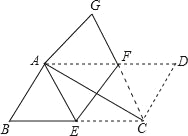
【答案】（1）詳見解析；（2）邊形AECF是菱形，理由詳見解析.
【解析】分析：（1）由四邊形ABCD是平行四邊形與折疊性質，易得AB=AG，∠BAE=∠GAF，∠BEA=∠EAF=∠GFA，則可利用AAS判定：△ABE≌△AGF．
（2）由（1）易證得EC=AE=AF，又由AF∥EC，即可判定四邊形AECF是菱形．
詳解：（1）∵四邊形ABCD是平行四邊形，∴AB=CD，∠BAD=∠BCD，由折疊的性質得：AG=CD，∠EAG=∠BCD，∴AB=AG，∠BAD=∠EAG，∴∠BAE=∠GAF．
又∵AB∥CD，AE∥GF，AD∥BC，∴∠BEA=∠EAF=∠GFA．在△ABE和△AGF中，∵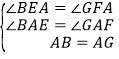
，∴△ABE≌△AGF（AAS）；
（2）四邊形AECF是菱形．理由如下：
由折疊的性質得：EC=AE．
∵△ABE≌△AGF，∴AE=AF，∴EC=AE=AF．
∵AF∥EC，∴四邊形AECF是平行四邊形，∴AECF是菱形．
同步學典一課多練系列答案
經典密卷系列答案
金牌課堂練系列答案科目：初中數學 來源： 題型：
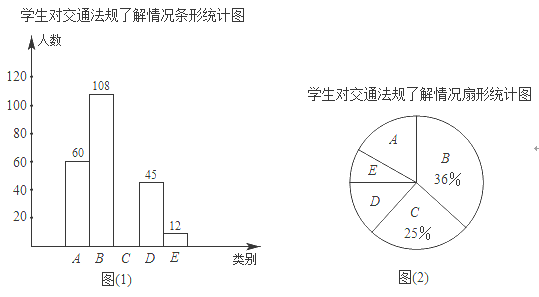
【題目】“機動車行駛到斑馬線要禮讓行人”等交通法規實施后，某校數學課外實踐小組就對這些交通法規的了解情況在全校隨機調査了部分學生，調查結果分為五種：A非常了解，B比較了解，C基本了解，D不太了解，E完全不知．實踐小組把此次調查結果整理并繪制成下面不完整的條形統計圖和扇形統計圖請根據以上信息，解答下列問題：
（1）本次共調查了 名學生，扇形統計圖中D所對應扇形的圓心角為 度；
（2）把這幅條形統計圖補充完整（畫圖后請標注相應的數據）；
（3）該校共有800名學生，根據以上信息，請你估計全校學生中對這些交通法規“非常了解”的有 名．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖中有四條互相不平行的直線L1、L2、L3、L4所截出的七個角．關于這七個角的度數關系，下列何者正確（ ）
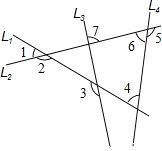
A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y＝ax2＋bx＋c經過A(－1，0)、B(3，0)、C(0，3)三點，直線l是拋物線的對稱軸．
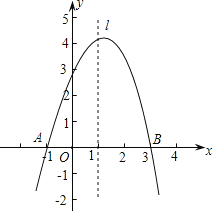
(1)求拋物線的函數關系式；
(2)設點P是直線l上的一個動點，當△PAC的周長最小時，求點P的坐標；
(3)在直線l上是否存在點M，使△MAC為等腰三角形？若存在，直接寫出所有符合條件的點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點O是直線CD上一點，OA, OB分別平分∠COE,∠DOE，
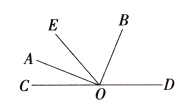
(1)寫出以O為頂點的2個角（除∠COE，∠DOE外）
(2)求∠AOB的度數
(3)如果
：
=1:3,求∠AOC和∠BOD的度數。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用同樣大小的圍棋子按如圖所示的方式擺圖案，按照這樣的規律擺下去，第12個圖案的圍棋子個數是（ ）
A. 16 B. 28 C. 29 D. 38
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】主題班會課上，王老師出示了如圖所示的一幅漫畫，經過同學們的一番熱議，達成以下四個觀點：
A.放下自我，彼此尊重； B.放下利益，彼此平衡；
C.放下性格，彼此成就； D.合理競爭，合作雙贏.
要求每人選取其中一個觀點寫出自己的感悟.根據同學們的選擇情況，小明繪制了下面兩幅不完整的圖表，請根據圖表中提供的信息，解答下列問題：
（1）參加本次討論的學生共有 人；
（2）表中
，
；
（3）將條形統計圖補充完整；
（4）現準備從
四個觀點中任選兩個作為演講主題，請用列表或畫樹狀圖的方法求選中觀點
（合理競爭，合作雙贏）的概率.
查看答案和解析>>
科目：初中數學 來源： 題型：
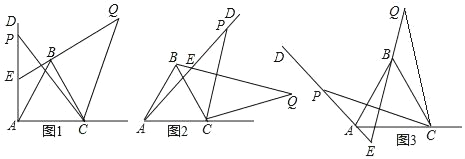
【題目】如圖1，已知∠DAC=90°，△ABC是等邊三角形，點P為射線AD上任意一點（點P與點A不重合），連結CP，將線段CP繞點C順時針旋轉60°得到線段CQ，連結QB并延長交直線AD于點E．
（1）如圖1，猜想∠QEP= °；
（2）如圖2，3，若當∠DAC是銳角或鈍角時，其它條件不變，猜想∠QEP的度數，選取一種情況加以證明；
（3）如圖3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
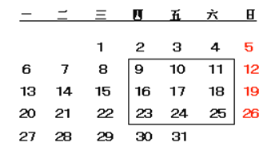
【題目】如圖：是某月份的月歷表，請你認真觀察月歷表，回答以下問題：
（1）如果圈出同一行的三個數，用a表示中間的數，則第一個數，第三個數怎樣表示？
（2）如果圈出同一列的三個數，用a表示中間的數，則第一個數，第三個數怎樣表示？
（3）如果圈出如圖所示的任意9個數，這9個數的和可能是207嗎？如果可能，請求出這9個數；如果不可能，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com