
已知關于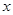 的方程
的方程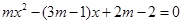 .
.
【小題1】求證:無論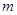 取任何實數時,方程恒有實數根;
取任何實數時,方程恒有實數根;
【小題2】若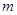 為整數,且拋物線
為整數,且拋物線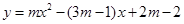 與
與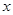 軸兩交點間的距離為2,求拋物線的解析式
軸兩交點間的距離為2,求拋物線的解析式
【小題3】若直線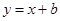 與(2)中的拋物線沒有交點,求
與(2)中的拋物線沒有交點,求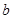 的取值范圍.
的取值范圍.
【小題1】分兩種情況討論.
① 當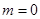 時,方程為
時,方程為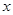
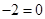
∴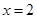 方程有實數根 -----------------------------1分
方程有實數根 -----------------------------1分
②當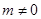 ,則一元二次方程的根的判別式
,則一元二次方程的根的判別式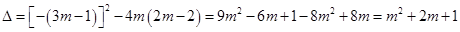
=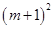
∴不論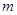 為何實數,
為何實數,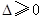 成立,
成立,
∴方程恒有實數根 -----------------------------------------3分
綜合①、②,可知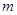 取任何實數,方程
取任何實數,方程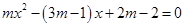 恒有實數根
恒有實數根
【小題2】設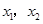 為拋物線
為拋物線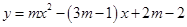 與
與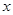 軸交點的橫坐標.
軸交點的橫坐標.
令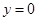 ,則
,則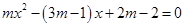
由求根公式得,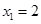 ,
,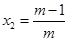 -------------------------------------5分
-------------------------------------5分
∴拋物線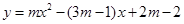 不論
不論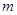 為任何不為0的實數時恒過定點
為任何不為0的實數時恒過定點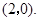 -----------------------6分
-----------------------6分
∵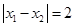
∴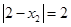
∴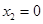 或
或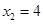 ,----------------------------------------------------------8分
,----------------------------------------------------------8分
∴ 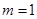 或
或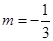 (舍去)
(舍去)
∴求拋物線解析式為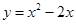 , ----------------------------------------9分
, ----------------------------------------9分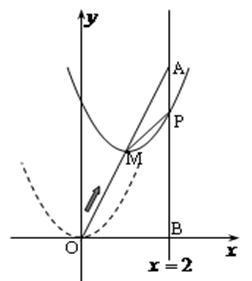
【小題3】由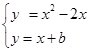 ,得
,得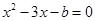
∴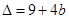 --------------------------------------10分
--------------------------------------10分
∵直線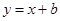 與拋物線
與拋物線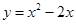 沒有交點
沒有交點
∴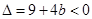
∴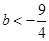 -------------------------------------11分
-------------------------------------11分
所以,當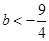 ,直線
,直線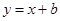 與(2)中的拋物線沒有交點. --------------12分
與(2)中的拋物線沒有交點. --------------12分
解析


科目:初中數學 來源: 題型:
 的方程
的方程 .
. 的取值范圍;
的取值范圍; 滿足
滿足 ,設二次函數
,設二次函數 的圖象與
的圖象與 軸交于
軸交于 兩點,將此圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,得到一個新的圖象.請你結合這個新的圖象回答:當直線
兩點,將此圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,得到一個新的圖象.請你結合這個新的圖象回答:當直線 與此圖象恰好有三個公共點時,求出
與此圖象恰好有三個公共點時,求出 的值(只需要求出兩個滿足題意的k值即可).
的值(只需要求出兩個滿足題意的k值即可).
查看答案和解析>>
科目:初中數學 來源:2011-2012學年九年級第一學期期中考試數學卷 題型:解答題
(本題6分)已知關于 的方程
的方程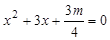 .
.
【小題1】(1)如果此方程有兩個不相等的實數根,求m的取值范圍;
【小題2】(2)在(1)中,若m為符合條件的最大整數,求此時方程的根.
查看答案和解析>>
科目:初中數學 來源:2012年北京市東城區中考二模數學試卷(帶解析) 題型:解答題
已知關于 的方程
的方程 .
.
【小題1】若方程有兩個不相等的實數根,求 的取值范圍;
的取值范圍;
【小題2】 若正整數 滿足
滿足 ,設二次函數
,設二次函數 的圖象與
的圖象與 軸交于
軸交于 兩點,將此圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,得到一個新的圖象.請你結合這個新的圖象回答:當直線
兩點,將此圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,得到一個新的圖象.請你結合這個新的圖象回答:當直線 與此圖象恰好有三個公共點時,求出
與此圖象恰好有三個公共點時,求出 的值(只需要求出兩個滿足題意的k值即可).
的值(只需要求出兩個滿足題意的k值即可).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com