
【題目】某班要從甲、乙兩名同學中選拔出一人,代表班級參加學校的一分鐘踢毽子體能素質比賽,在一段時間內的相同條件下,甲、乙兩人進行了六場一分鐘踢毽子的選拔測試,根據他們的成績繪制出如圖的統計表和不完整的折線統計圖.
甲、乙兩人選拔測試成績統計表
甲成績 | 乙成績 | |
第1場 | 87 | 87 |
第2場 | 94 | 98 |
第3場 | 91 | 87 |
第4場 | 85 | 89 |
第5場 | 91 | 100 |
第6場 | 92 | 85 |
中位數 | 91 | n |
平均數 | m | 91 |
并計算出乙同學六場選拔測試成績的方差:
S乙2= ![]() =
= ![]()
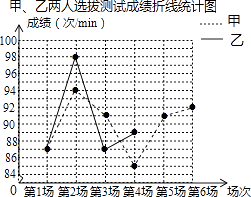
(1)m= , n= , 并補全全圖中甲、乙兩人選拔測試成績折線統計圖;
(2)求甲同學六場選拔測試成績的方差S甲2;
(3)分別從平均數、中位數和方差的角度分析比較甲、乙二人的成績各有什么特點?
(4)經查閱該校以往本項比賽的資料可知,①成績若達到90次/min,就有可能奪得冠軍,你認為選誰參賽更有把握奪冠?為什么?
②該項成績的最好記錄是95次/min,就有可能奪得冠軍,你認為選誰參賽更有把握奪冠?為什么?
【答案】
(1)90,88解:如圖所示: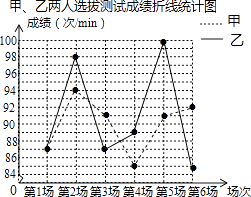
(2)解:∵m=90,
∴S甲2= ![]() =
= ![]()
(3)解:從平均數看,一的平均數大于甲的平均數,說明乙成績的平均水平比甲高,
從中位數看,甲的中位數大于乙的中位數,說明甲較高成績的次數比乙多,
從方差看,甲的方差小于乙的方差,說明甲的成績比乙的更穩定
(4)解:①選取甲參賽更有把握奪得冠軍,
理由:在6場比賽中,甲有4場比賽成績超過90次/min,而乙只有2場,且甲的方差小于乙的方差,成績更穩定,故答案為:甲參賽更有把握奪得冠軍;
②選乙參賽更有把握奪得冠軍,
理由:在比賽中,乙有2場成績超過95次/min,而甲一次也沒有,故答案為:乙參賽更有把握奪得冠軍.
【解析】解:(1)由表格可得,
m= ![]() =90,
=90,
將乙6場的成績按從小到大排列是:85,87,87,89,98,100,
∴n= ![]() =88,
=88,
所以答案是:90,88;
【考點精析】關于本題考查的折線統計圖和算術平均數,需要了解能清楚地反映事物的變化情況,但是不能清楚地表示出在總體中所占的百分比;總數量÷總份數=平均數.解題關鍵是根據已知條件確定總數量以及與它相對應的總份數才能得出正確答案.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知射線CB//OA,∠C=∠OAB=100°,E、F在CB上,且滿足∠FOB=∠AOB,OE平分∠COF.
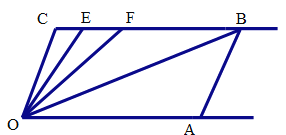
(1)求∠EOB的度數.(直接寫出結果,無需解答過程)
∠EOB=__________°
(2)若在OC右側左右平行移動AB,那么∠OBC:∠OFC的值是否隨之發生變化?若變化,請找出變化規律;若不變,請求出這個比值.
(3)在OC右側左右平行移動AB的過程中,是否存在使∠OEC=∠OBA的情況?若存在,請直接寫出∠OEC度數;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,射線
,射線![]() 分別和直線
分別和直線![]() 交于點
交于點![]() ,射線
,射線![]() 分別和直線
分別和直線![]() 交于點
交于點![]() ,點
,點![]() 在射線
在射線![]() 上運動(
上運動(![]() 點與
點與![]() 三點不重合),設
三點不重合),設![]() ,
,![]() ,
,![]() .
.

(1)如果點![]() 在
在![]() 兩點之間運動時,
兩點之間運動時,![]() 之間有何數量關系?請說明理由;
之間有何數量關系?請說明理由;
(2)如果點![]() 在
在![]() 兩點之外運動時,
兩點之外運動時,![]() 之間有何數量關系?(只需寫出結論,不必說明理由)
之間有何數量關系?(只需寫出結論,不必說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,對于二次函數y=ax2+bx+c(a≠0)的圖象,得出了下面五條信息:①c>0;②b=6a;③b2﹣4ac>0;④a+b+c<0;⑤對于圖象上的兩點(﹣6,m )、(1,n),有m<n.其中正確信息的個數有( )
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,已知AD∥BC,AB⊥BC,點E,F在邊AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
.
(1)BC= ;
(2)求點D到BC的距離;
(3)求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形BCDE的各邊分別平行于x軸與y軸,物體甲和物體乙由點A(2,0)同時出發,沿矩形BCDE的邊作環繞運動,物體甲按逆時針方向以1個單位/秒勻速運動,物體乙按順時針方向以2個單位/秒勻速運動,則兩個物體運動后的第2019次相遇地點的坐標是( )

A. (1,﹣1)B. (2,0)C. (﹣1,1)D. (﹣1,﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三位同學分別正確指出了某一個函數的一個性質.甲:函數圖象經過第一象限;乙:函數圖象經過第三象限;丙:每第一個象限內,y值隨x值的增大而減小.根據他們的描述,這個函數表達式可能是( )
A.y=2x
B.y= ![]()
C.y=﹣ ![]()
D.y=2x2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學對多項式(x2-4x-3)(x2-4x+1)+4進行因式分解的過程.
解:設x2-4x=y
原式=(y-3)(y+1)+4 (第一步)
= y2-2y+1 (第二步)
=(y-1)2 (第三步)
=(x2-4x-1)2 (第四步)
回答下列問題:
(1)該同學第二步到第三步運用了因式分解的_______.
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)請你模仿以上方法嘗試對多項式(x2+2x)(x2+2x+2)+1進行因式分解.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com