【題目】根據下列條件，能畫出唯一△ABC的是（ ）
A.AB＝4，BC＝5，AC＝1B.AB＝5，BC＝4，∠A＝40°
C.∠A＝60°，∠B＝50°，AB＝5D.∠C＝90°，AB＝8
【答案】C
【解析】
要滿足唯一畫出△ABC，就要求選項給出的條件符合三角形全等的判定方法，不符合判定方法的畫出的圖形不一樣，也就是三角形不唯一，而各選項中只有C選項符合ASA，是滿足題目要求的，于是答案可得
A、因為AB+ AC= BC，所以這三邊不能構成三角形，故本選項不符合題意；
B、根據AB=5，BC=4，∠A=40°不能畫出唯一三角形，如圖所示△ABD和△ABC，故本選項不符合題意；
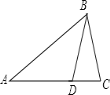
C、根據∠A=60°，∠B=50°，AB=5，符合全等三角形的判定定理ASA，即能畫出唯一三角形，故本選項正確；
D、只有一個角和一個邊無法根據此作出一個唯一的三角形，故本選項不符合題意；
故選：C
根據題意得，
長江作業本同步練習冊系列答案科目：初中數學 來源： 題型：
【題目】（1）|﹣3|﹣5×（﹣
）+（﹣4）
（2）（﹣2）2﹣4÷（﹣
）+（﹣1）2016
（3）
×（﹣24）
（4）﹣12014﹣（1﹣0.5）÷
×[（﹣2）3﹣4]
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，大樓AB右側有一障礙物，在障礙物的旁邊有一幢小樓DE，在小樓的頂端D處測得障礙物邊緣點C的俯角為300，測得大樓頂端 A的仰角為450（點B,C,E在同一水平直線上）。已知AB=50m,DE=10m,求障礙物B,C兩點間的距離。（結果精確到1m,參考數據： 
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一輛汽車在某次行駛過程中，油箱中的剩余油量
（升）與行駛路程
（千米）之間是一次函數關系，其部分圖象如圖所示.
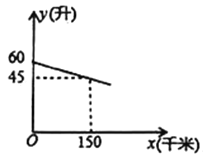
（1）求關于的函數關系式；（不需要寫自變量的取值范圍）
（2）已知當油箱中的剩余油量為10升時，該汽車會開始提示加油，在此次行駛過程中，行駛了482千米時，司機發現離前方最近的加油站有30千米的路程，在開往該加油站的途中，汽車開始提示加油，這時離加油站的路程是多少千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】解答下列問題：
（1）計算：6÷(－
＋
)．
方方同學的計算過程如下：原式＝6÷(－
)＋6÷
＝－12＋18＝6．
請你判斷方方同學的計算過程是否正確，若不正確，請你寫出正確的計算過程．
（2）請你參考黑板中老師的講解，用運算律簡便計算（請寫出具體的解題過程）：
①999×（-15）；②999×
+333×（-
）-999×
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點P是∠AOB平分線上一點，PC⊥OA，PD⊥OB，垂足為C，D.
(1)∠PCD＝∠PDC嗎？為什么？
(2)OP是CD的垂直平分線嗎？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，數軸上A，B兩點表示的數分別為-4，8.有一動點P從點A出發，第1次向左運動1個單位長度，第2次向右運動2個單位長度，第3次向左運動3個單位長度……按照此規律不斷地運動.
（1）①當運動到第2020次時，點P表示的數是_______；
②點A與點B的距離AB=_______；
（2）點P會不會在某次運動時恰好到達某一個位置，使點P到點B的距離是點P到點A的距離的3倍？若存在，請求出此時點P表示的數；若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場用24000元購入一批空調，然后以每臺3000元的價格銷售，因天氣炎熱，空調很快售完；商場又以52000元的價格再次購入該種型號的空調，數量是第一次購入的2倍，但購入的單價上調了200元，售價每臺也上調了200元．
（1）商場第一次購入的空調每臺進價是多少元？
（2）商場既要盡快售完第二次購入的空調，又要在這兩次空調銷售中獲得的利潤率不低于22%，打算將第二次購入的部分空調按每臺九五折出售，最多可將多少臺空調打折出售？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算題
（1）解方程組：
① 
②
（2）計算
①(π-2013)0-(
)-2+|-4|；
②4(a+2)(a+1)-7(a+3)(a-3)
（3）因式分解
①a4－16
②
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com