
【題目】綜合題
(1)操作發現:
如圖①,在正方形ABCD中,過A點有直線AP,點B關于AP的對稱點為E,連接DE交AP于點F,當∠BAP=20°時,則∠AFD=°;當∠BAP=α°(0<α<45°)時,則∠AFD=;猜想線段DF,EF,AF之間的數量關系:DF﹣EF=AF(填系數);
(2)數學思考:
如圖②,若將“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他條件不變,則∠AFD=;線段DF,EF,AF之間的數量關系是否發生改變,若發生改變,請寫出數量關系并說明理由;
(3)類比探究:
如圖③,若將“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他條件不變,則∠AFD=°;請直接寫出線段DF,EF,AF之間的數量關系: .
【答案】
(1)45,![]() ,45
,45
(2)30
(3)解:(90﹣ ![]() ),DF﹣EF=2sin
),DF﹣EF=2sin ![]() αAF
αAF
【解析】【解析】解:(1)如圖①中,連接BF、作AH⊥AF交DE于H.
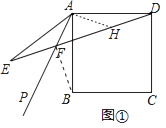
當∠PAB=20°時,
∵∠PAB=∠PAE=20°,∠BAD=90°,
∴∠EAD=130°,
∵AB=AE=AD,
∴∠E= ![]() (180°﹣130°)=25°,
(180°﹣130°)=25°,
∴∠AFD=∠E+∠PAE=45°,
當∠PAB=α時,∠E= ![]() [180°﹣(90°+2α)]=45°﹣α,
[180°﹣(90°+2α)]=45°﹣α,
∴∠AFD=∠E+∠PAE=45°﹣α+α=45°,
∵∠AFH=45°,∠FAH=90°,
∴AF=AH,
∵∠FAH=∠BAD=90°,
∴∠FAB=∠HAD,∵AB=AD,
∴△FAB≌△HAD,
∴BF=DH,
∵EF=BF,
∴DH=EF,
∴DF﹣EF=FH= ![]() AF,
AF,
所以答案是45,45, ![]() .
.
⑵如圖②中,連接BF、作∠FAH=120°交DE于H,AM⊥DE于M.
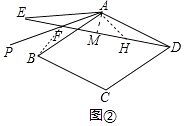
設∠PAB=α,
則∠E= ![]() [180°﹣(120°+2α)=30°﹣α,
[180°﹣(120°+2α)=30°﹣α,
∴∠AFD=∠E+∠PAE=30°,
∵∠EAH=∠BAD=120°,
∴∠FAB=∠HAD,
∵∠AFH=∠AHF=30°,
∴AF=AH,∵AB=AD,
∴△FAB≌△HAD,
∴BF=DH=EF,
∴DF﹣AF=DF﹣DH=FH,
∴AM⊥FH,AF=AH,
∴FM=MH=AFcos30°,
∴FH= ![]() AF,
AF,
∴DF﹣EF= ![]() AF,
AF,
所以答案是30,改變,DF﹣EF= ![]() AF
AF
⑶如圖③中,當∠BAD=α時,設∠PAB=∠PAE=x,連接BF、作∠FAH=α交DE于H,AM⊥DE于M.
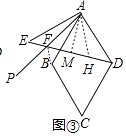
則∠E= ![]() [180°﹣(α+2x)=90°﹣
[180°﹣(α+2x)=90°﹣ ![]() α﹣x,
α﹣x,
∴∠AFD=∠E+∠PAE=90°﹣ ![]() α,
α,
∵∠EAH=∠BAD=α,
∴∠FAB=∠HAD,
∵∠AFH=∠AHF=90°﹣ ![]() α,
α,
∴AF=AH,∵AB=AD,
∴△FAB≌△HAD,
∴BF=DH=EF,
∴DF﹣AF=DF﹣DH=FH,
∴AM⊥FH,AF=AH,
∴FM=MH=AFsin ![]() α,
α,
∴FH=2sin ![]() αAF,
αAF,
∴DF﹣EF=2sin ![]() αAF.
αAF.
所以答案是(90﹣ img src="http://thumb.zyjl.cn/questionBank/Upload/2018/02/24/01/d9b95732/SYS201802240151098887506597_DA/SYS201802240151098887506597_DA.002.png" width="9" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ),DF﹣EF=2sin ![]() αAF.
αAF.
(1)如圖①中,連接BF、作AH⊥AF交DE于H.根據∠AFD=∠E+∠PAE=45°求出∠E即可解決問題;只需要證明△FAB≌△HAD,就可得出結論DF﹣EF=FH=![]() AF解決問題;(2)如圖②中,結論:30°,改變,DF﹣EF=
AF解決問題;(2)如圖②中,結論:30°,改變,DF﹣EF= ![]() AF,連接BF、作∠FAH=120°交DE于H,AM⊥DE于M.只需要證明△FAB≌△HAD,FH=
AF,連接BF、作∠FAH=120°交DE于H,AM⊥DE于M.只需要證明△FAB≌△HAD,FH= ![]() AF即可;(3)結論(90﹣
AF即可;(3)結論(90﹣ ![]() ),DF﹣EF=2sin
),DF﹣EF=2sin ![]() αAF.如圖③中,當∠BAD=α時,設∠PAB=∠PAE=x,連接BF、作∠FAH=α交DE于H,AM⊥DE于M.證明方法類似。
αAF.如圖③中,當∠BAD=α時,設∠PAB=∠PAE=x,連接BF、作∠FAH=α交DE于H,AM⊥DE于M.證明方法類似。
【考點精析】認真審題,首先需要了解菱形的性質(菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半),還要掌握正方形的性質(正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】為了解學生的藝術特長發展情況,某校音樂決定圍繞在“舞蹈、樂器、聲樂、戲曲、其他活動”項目中,你最喜歡哪一項活動(每人只限一項)的問題,在全校范圍內隨機抽取部分學生進行問卷調查,并將調查結果繪制如下兩幅不完整的統計圖.請你根據統計圖解答下列問題:
(1)在這次調查中,一共抽查了名學生,其中喜歡“舞蹈”活動項目的人數占抽查總人數的百分比為 . 扇形統計圖中喜歡“戲曲”部分扇形的圓心角為度.
(2)請你補全條形統計圖.
(3)若在“舞蹈、樂器、聲樂、戲曲”項目中任選兩項成立課外興趣小組,請用列表或畫樹狀圖的方法求恰好選中“舞蹈、聲樂”這兩項的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:點C在線段BD上,AC⊥CE,∠A=∠1,∠E=∠2.
(1)若∠1=70°,求∠B、∠D的度數;
(2)判斷AB與ED的位置關系,并說明理由;
(3)作∠A、∠E的角平分線相交于點P,求∠P的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,且AB=6,C是⊙O上一點,D是 ![]() 的中點,過點D作⊙O的切線,與AB,AC的延長線分別交于點E,F,連接AD.
的中點,過點D作⊙O的切線,與AB,AC的延長線分別交于點E,F,連接AD.
(1)求證:AF⊥EF;
(2)填空:
①當BE=時,點C是AF的中點;
②當BE=時,四邊形OBDC是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵市民節約用水,某市居民生活用水按階梯式水價計費.下表是該市民居民“一戶一表”生活用水階梯式計費價格表的部分信息:

(說明:①每戶產生的污水量等于該戶自來水用水量;②水費=自來水費用+污水處理費)
已知小王家2012年4月用水20噸,交水費66元,5月份用水25噸,交水費91元.
(1)求a,b的值;
(2)隨著夏天的到來,用水量將增加.為了節省開支.小王計劃把6月份的水費控制在不超過家庭月收入的2%,若小王家的月收入為9200元,則小王家6月份最多能用水多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,BE平分∠ABC,點P在射線BE上.

(1)如圖1,若∠ABC=40°,CP∥AB,求∠BPC的度數;
(2)如圖2,若∠BAC=100°,∠PBC=∠PCA,求∠BPC的度數;
(3)若∠ABC=40°,∠ACB=30°,直線CP與△ABC的一條邊垂直,畫出相應圖形并求∠BPC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中華文明,源遠流長;中華漢字,寓意深廣,為了傳承優秀傳統文化,某校團委組織了一次全校3000名學生參加的“漢字聽寫”大賽,賽后發現所有參賽學生的成績均不低于50分.為了更好地了解本次大賽的成績分布情況,隨機抽取了其中200名學生的成績(成績x取整數,總分100分)作為樣本進行整理,得到下列不完整的統計圖表:
成績x/分 | 頻數 | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
請根據所給信息,解答下列問題:
(1)m= ,n= ;
(2)請補全頻數分布直方圖;
(3)若成績在90分以上(包括90分)的為“優”等,則該校參加這次比賽的3000名學生中成績“優”等約有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】各頂點都在方格紙格點(橫豎格子線的交錯點)上的多邊形稱為格點多邊形.如何計算它的面積?奧地利數學家皮克證明了格點多邊形的面積公式:![]() ,其中
,其中![]() 表示多邊形內部的格點數,
表示多邊形內部的格點數,![]() 表示多邊形邊界上的格點數,
表示多邊形邊界上的格點數,![]() 表示多邊形的面積.如圖①,
表示多邊形的面積.如圖①,![]()
![]()

(1)請算出圖②中格點多邊形的面積是 .
(2)請在圖③中畫一個格點平行四邊形,使它的面積為7,且每條邊上除頂點外無其他格點.
(3)請在圖④中畫一個格點菱形(非正方形),使它內部和邊界上都只含有4個格點,并算出它的面積是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了測量某建筑物BC的高度,小明先在地面上用測角儀自A處測得建筑物頂部的仰角是30°,然后在水平地而上向建筑物前進了50m到達D處,此時遇到一斜坡,坡度i=1: ![]() ,沿著斜坡前進20米到達E處測得建筑物頂部的仰角是45°,(坡度i=1:
,沿著斜坡前進20米到達E處測得建筑物頂部的仰角是45°,(坡度i=1: ![]() 是指坡面的鉛直高度FE與水平寬度DE的比).請你計算出該建筑物BC的高度.(取
是指坡面的鉛直高度FE與水平寬度DE的比).請你計算出該建筑物BC的高度.(取 ![]() =1.732,結果精確到0.1m).
=1.732,結果精確到0.1m).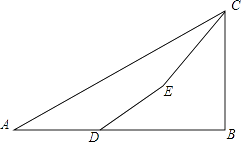
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com