【答案】
分析:(1)把點A與頂點坐標代入拋物線解析式進行計算求出a、b的值,然后即可得解;
(2)聯立直線y=-3與拋物線解析式求出點B、C的坐標,然后求出BC的長度,再根據平行四邊形的面積公式列式計算即可得解;
(3)先根據平行四邊形的面積求出點P到BC的距離,然后求出點P的縱坐標,再代入拋物線解析進行計算求出點P的橫坐標,從而得解;
(4)根據拋物線解析式設點P的坐標為(x,-x
2-2x),然后分①點P在BC邊的上方時,表示出點P到BC的距離,然后根據二次函數的增減性求出距離的最大值,②點P在BC的下方時,表示出點P到BC的距離,然后根據二次函數的增減性求出距離的最大值,然后二者比較,從而得解.
解答: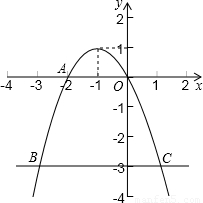
解:(1)∵拋物線y=ax
2+bx經過點A(-2,0),頂點為(-1,1),
∴

,
解得
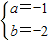
,
∴拋物線的解析式為y=-x
2-2x;
(2)聯立
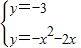
,
解得
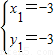
,

,
∵B點在C點左側,
∴點B(-3,-3),C(1,-3),
∴BC=1-(-3)=1+3=4,
又∵平行四邊形以BC為一邊,原點O為另一頂點,
∴S=4×3=12;
(3)設點P到BC的距離為h,
則BC•h=8,
即4h=8,
解得h=2,
①當點P在BC的上方時,點P的縱坐標為-3+2=-1,
此時,-x
2-2x=-1,
整理得,x
2+2x-1=0,
解得x
1=-1-
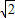
,x
2=-1+
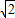
,
所以,點P的坐標為(-1-
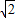
,-1)或(-1+
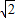
,-1),
②當點P在BC下方時,點P的縱坐標為-3-2=-5,
此時,-x
2-2x=-5,
整理得,x
2+2x-5=0,
解得x
1=-1-

,x
2=-1+
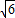
,
所以,點P的坐標為(-1-

,-5)或(-1+

,-5);
綜上所述,平行四邊形面積為8時,點P的坐標為(-1-
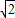
,-1)或(-1+
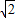
,-1)或(-1-
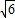
,-5)或(-1+
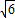
,-5);
(4)設點P的坐標為(x,-x
2-2x),
①點P在BC邊的上方時,點P到BC的距離為-x
2-2x-(-3)=-x
2-2x+3=-(x+1)
2+4,
∵點B(-3,-3),C(1,-3),
∴x的取值范圍為-3<x<1,
∴當x=-1時,距離有最大值,為4,
②點P在BC的下方時,點P到BC的距離為-3-(-x
2-2x)=x
2+2x-3=(x+1)
2-3,
∵點B(-3,-3),C(1,-3),
∴在-4≤x≤2范圍內,x的取值范圍為-4≤x<3或1<x≤2,
∴當x=-4或x=2時,距離有最大值,為(-4+1)
2-3=5,
∵5>4,
∴當點P在BC的下方時,在-4≤x≤2范圍內,平行四邊形的面積有最大值,
最大值為:4×5=20,
此時,-x
2-2x=-(-4)
2-2×(-4)=-16+8=-8,
-x
2-2x=-2
2-2×2=-4-4=-8,
所以點P的坐標為(-4,-8)或(2,-8),
故,存在點P(-4,-8)或(2,-8),使在-4≤x≤2范圍內,平行四邊形的面積有最大值.
點評:本題考查了二次函數綜合題型,主要涉及待定系數法求二次函數解析式,平行四邊形的面積,二次函數的最值問題,難點在于(3)(4)兩題要分情況進行討論求解.

 解:(1)∵拋物線y=ax2+bx經過點A(-2,0),頂點為(-1,1),
解:(1)∵拋物線y=ax2+bx經過點A(-2,0),頂點為(-1,1), ,
,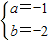 ,
,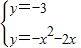 ,
,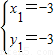 ,
, ,
,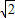 ,x2=-1+
,x2=-1+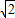 ,
,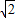 ,-1)或(-1+
,-1)或(-1+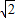 ,-1),
,-1), ,x2=-1+
,x2=-1+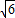 ,
, ,-5)或(-1+
,-5)或(-1+ ,-5);
,-5);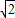 ,-1)或(-1+
,-1)或(-1+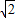 ,-1)或(-1-
,-1)或(-1-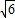 ,-5)或(-1+
,-5)或(-1+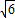 ,-5);
,-5);

 閱讀快車系列答案
閱讀快車系列答案 與x軸的另一個交點為E.
與x軸的另一個交點為E. 如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=
如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=