
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,
,![]() 是
是![]() 上一點,經過
上一點,經過![]() ,
,![]() 兩點的
兩點的![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,作
,作![]() 的平分線
的平分線![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
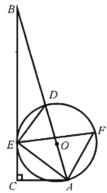
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
【答案】(1)見解析;(2)AC=6.4
【解析】
(1)連接OE,根據同圓的半徑相等和角平分線可得:OE∥AC,則∠BEO=∠C=90°,解決問題;
(2)過A作AH⊥EF于H,根據三角函數先計算![]() ,證明△AEH是等腰直角三角形,則AE=
,證明△AEH是等腰直角三角形,則AE=![]() AH=8,證明△AED∽△ACE,得到
AH=8,證明△AED∽△ACE,得到![]() 即可解決問題.
即可解決問題.
證明:(1)連接OE,
∵OE=OA,
∴∠OEA=∠OAE,
∵AE平分∠BAC,
∴∠OAE=∠CAE,
∴∠CAE=∠OEA,
∴OE∥AC,
∴∠BEO=∠C=90°,
∴BC是⊙O的切線;
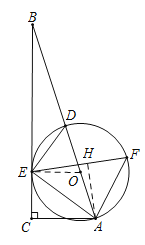
(2)過A作AH⊥EF于H,
![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AD是⊙O的直徑,
∴∠AED=90°,
∵EF平分∠AED,
∴∠AEF=45°,
∴△AEH是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AC=6.4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
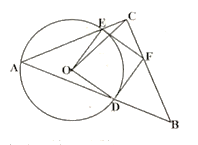
【題目】如圖,等腰![]() 的一個銳角頂點
的一個銳角頂點![]() 是
是![]() 上的一個動點,
上的一個動點,![]() ,腰
,腰![]() 與斜邊
與斜邊![]() 分別交
分別交![]() 于點
于點![]() ,分別過點
,分別過點![]() 作
作![]() 的切線交于點
的切線交于點![]() ,且點
,且點![]() 恰好是腰
恰好是腰![]() 上的點,連接
上的點,連接![]() ,若
,若![]() 的半徑為4,則
的半徑為4,則![]() 的最大值為:( )
的最大值為:( )
A.![]() B.
B.![]() C.6D.8
C.6D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
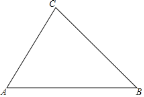
【題目】如圖,已知△ABC,請用直尺(不帶刻度),和圓規,按下列要求作圖(不要求寫作法,但要保留作圖痕跡).
(1)作菱形AMNP,使點M,N、P在邊AB、BC、CA上;
(2)當∠A=60°,AB=4,AC=3時,求菱形AMNP的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司用6000元購進A,B兩種電話機25臺,購買A種電話機與購買B種電話機的費用相等.已知A種電話機的單價是B種電話機單價的1.5倍.
(1)求A,B兩種電話機的單價各是多少?
(2)若計劃用不超過8000元的資金再次購進A,B兩種話機共30臺,已知A,B兩種電話機的進價不變,求最多能購進多少臺A種電話機?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() 連接
連接![]() 點
點![]() 是第一象限內拋物線上的一個動點,點
是第一象限內拋物線上的一個動點,點![]() 的橫坐標為
的橫坐標為![]() ,過點
,過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() 交
交![]() 于點
于點![]() 過點
過點![]() 作
作![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() .
.
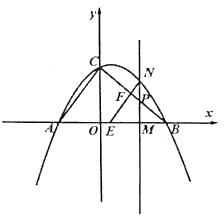
(1)求![]() 三點的坐標;
三點的坐標;
(2)試探究在點![]() 運動過程中,是否存在這樣的點
運動過程中,是否存在這樣的點![]() 使得以點
使得以點![]() 為頂點的三角形是等腰三角形,若存在,請求出此時點
為頂點的三角形是等腰三角形,若存在,請求出此時點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
(3)m是點![]() 的橫坐標,請用含
的橫坐標,請用含![]() 的代數式表示線段
的代數式表示線段![]() 的長,并求出
的長,并求出![]() 為何值時
為何值時![]() 有最大值.
有最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,以AB為直徑的半圓O經過點C,D.AC與BD相交于點E,CD2=CE·CA,分別延長AB,DC相交于點P,PB=BO,CD=2![]() .則BO的長是_________.
.則BO的長是_________.
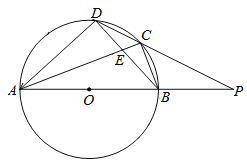
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學就“戲曲進校園”活動的喜愛情況進行了隨機調查,對收集的信息進行了統計,繪制了下面兩幅尚不完整的統計圖.請你根據統計圖所提供的信息解答下列問題:(圖中![]() 表示“很喜歡”,
表示“很喜歡”,![]() 表示“喜歡”,
表示“喜歡”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜歡”)
表示“不喜歡”)
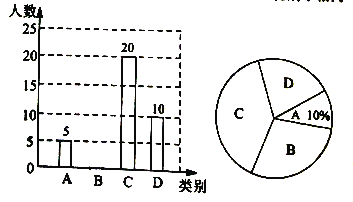
(1)被調查的總人數是_________,扇形統計圖中![]() 部分所對應的扇形圓心角的度數為_________;
部分所對應的扇形圓心角的度數為_________;
(2)補全條形統計圖;
(3)在抽取的![]() 類5人中,剛好有甲、乙、丙3個女生和丁、戊2個男生,從中隨機抽取兩個同學擔任兩角色,用畫樹狀圖或列表法求出抽到的兩個學生性別不相同的概率.
類5人中,剛好有甲、乙、丙3個女生和丁、戊2個男生,從中隨機抽取兩個同學擔任兩角色,用畫樹狀圖或列表法求出抽到的兩個學生性別不相同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. 一個游戲的中獎概率是10%,則做10次這樣的游戲一定會中獎
B. 為了解全國中學生的心理健康情況,應該采用普查的方式
C. 若甲組數據的方差S甲2=0.01,乙組數據的方差S乙2=0.1,則乙組數據比甲組數據穩定
D. 一組數據8,3,7,8,8,9,10的眾數和中位數都是8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com