
【題目】二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),將二次函數
的左側),將二次函數![]() 的圖象繞點
的圖象繞點![]() 旋轉180度得到圖象為
旋轉180度得到圖象為![]() ,當
,當![]() 時,圖象
時,圖象![]() 上點
上點![]() 縱坐標的最小值為
縱坐標的最小值為![]() ,則
,則![]() _________.
_________.
【答案】5
【解析】
根據二次函數解析式可求出A、B兩點坐標,設圖象G的解析式為y=-x2+bx+c,A點的對應點為A′,根據旋轉的性質可求出點A′的坐標,把A′、B坐標代入可求出b、c的值,即可得圖象G的解析式,可求出圖象G的對稱軸,根據二次函數的增減性即可得答案.
∵二次函數y=x2-4x-5的圖象與x軸交于A、B兩點(點A在點B的左側),
∴y=0時,x2-4x-5=0,
解得x1=-1,x2=5,
∴A(-1,0),B(5,0),
∵將二次函數y=x2-4x-5的圖象繞點B旋轉180度得到圖象為G,
∴設圖象G的解析式為y=-x2+bx+c,A點的對應點為A′,
∴點A′坐標為(11,0),
把B、A′坐標代入y=-x2+bx+c得:![]() ,
,
解得:![]() ,
,
∴圖象G點解析式為y=-x2+16x-55=-(x-8)2+9,
∴圖象G的對稱軸為直線x=8,
∵-1<0,
∴拋物線點開口向下,
∵9-8<8-6,
∴當![]() 時,x=6為函數最小值,
時,x=6為函數最小值,
∴點C縱坐標y=-36+96-55=5,
故答案為:5


科目:初中數學 來源: 題型:
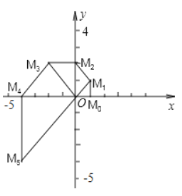
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,將線段
,將線段![]() 繞原點
繞原點![]() 逆時針方向旋轉
逆時針方向旋轉![]() ,再將其延長至點
,再將其延長至點![]() ,使得
,使得![]() ,得到線段
,得到線段![]() ;又將線段
;又將線段![]() 繞原點
繞原點![]() 逆時針方向旋轉
逆時針方向旋轉![]() ,再將其延長至點
,再將其延長至點![]() ,使得
,使得![]() ,得到線段
,得到線段![]() ;如此下去,依次得到線段
;如此下去,依次得到線段![]() 、
、![]() 、
、![]() 、…根據以上規律,線段
、…根據以上規律,線段![]() 的長度為__
的長度為__
查看答案和解析>>
科目:初中數學 來源: 題型:
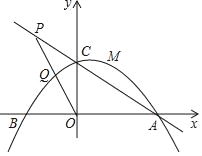
【題目】如圖,拋物線y=﹣![]() (其中m>0)與x軸分別交于A,B兩點(A在B的右側),與y軸交于點c.
(其中m>0)與x軸分別交于A,B兩點(A在B的右側),與y軸交于點c.
(1)求△AOC的周長,(用含m的代數式表示)
(2)若點P為直線AC上的一點,且點P在第二象限,滿足OP2=PCPA,求tan∠APO的值及用含m的代數式表示點P的坐標;
(3)在(2)的情況下,線段OP與拋物線相交于點Q,若點Q恰好為OP的中點,此時對于在拋物線上且介于點C與拋物線頂點之間(含點C與頂點)的任意一點M(x0,y0)總能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范圍.
恒成立,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某建筑物![]() 上掛著“巴山渝水,魅力重慶”的宣傳條幅
上掛著“巴山渝水,魅力重慶”的宣傳條幅![]() ,王同學利用測傾器在斜坡的底部
,王同學利用測傾器在斜坡的底部![]() 處測得條幅底部
處測得條幅底部![]() 的仰角為60°,沿斜坡AB走到B處測得條幅頂部C的仰角為50°.已知斜坡
的仰角為60°,沿斜坡AB走到B處測得條幅頂部C的仰角為50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(點
米(點![]() 在同平面內,
在同平面內,![]() ,測傾器的高度忽略不計),則條幅
,測傾器的高度忽略不計),則條幅![]() 的長度約為(參考數據:
的長度約為(參考數據:![]()
![]() )
)
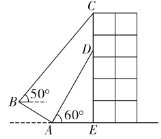
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在初中階段的函數學習中,我們經歷了“確定函數的表達式——利用函數圖象研究其性質——應用函數解決問題”的學習過程.在畫函數圖象時,我們可以通過描點或平移的方法畫出一個函數的大致圖象,結合上面經歷的學習過程,現在來解決下面問題:
在函數![]() 中,當
中,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
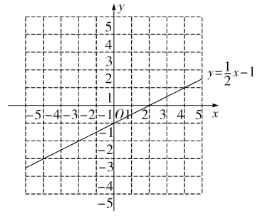
(1)求這個函數的表達式;
(2)在給出的平面直角坐標系中,請用你喜歡的方法畫出這個函數的圖象,并寫出這個函數的一條性質;
(3)已知函數![]() 的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式
的圖象如圖所示,結合你所畫的函數圖象,直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,二次函數![]() 的函數解析式為
的函數解析式為![]() ,點
,點![]() 是二次函數
是二次函數![]() 的圖象上一點,過點
的圖象上一點,過點![]() 作直線
作直線![]() 軸,且點
軸,且點![]() 的橫坐標為
的橫坐標為![]() ,二次函數
,二次函數![]() 的圖象與二次函數
的圖象與二次函數![]() 的圖象關于直線
的圖象關于直線![]() 成軸對稱.
成軸對稱.

(1)直接寫出二次函數![]() 圖象的對稱軸(用含
圖象的對稱軸(用含![]() 的代數式表示)
的代數式表示)
(2)當點![]() 落在
落在![]() 軸上時,求二次函數
軸上時,求二次函數![]() 的解析式.
的解析式.
(3)當點![]() 在
在![]() 軸的右側時,過點
軸的右側時,過點![]() 作射線
作射線![]() 軸,設射線
軸,設射線![]() 與
與![]() 的圖象交于點
的圖象交于點![]() ,
,![]() 的圖象在
的圖象在![]() 上方的部分記為
上方的部分記為![]() ,
,![]() 的圖象的剩余部分沿
的圖象的剩余部分沿![]() 翻折得到
翻折得到![]() ,由
,由![]() 和
和![]() 所組成的圖象記為
所組成的圖象記為![]() .
.
①當點![]() 的縱坐標與橫坐標之和為6時,求
的縱坐標與橫坐標之和為6時,求![]() 的值
的值
②當![]() 時,隨著
時,隨著![]() 的增大,圖象
的增大,圖象![]() 所對應函數的函數值
所對應函數的函數值![]() 先減小后增大時,直接寫出
先減小后增大時,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
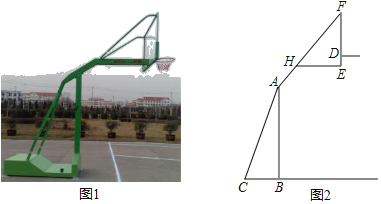
【題目】如圖1,2分別是某款籃球架的實物圖與示意圖,AB⊥BC于點B,底座BC=1.3米,底座BC與支架AC所成的角∠ACB=60°,點H在支架AF上,籃板底部支架EH∥BC.EF⊥EH于點E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求籃板底部支架HE與支架AF所成的∠FHE的度數.
(2)求籃板底部點E到地面的距離,(精確到0.01米)(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五一期間,甲、乙兩人在附近的景點游玩,甲從![]() 、
、![]() 、
、![]() 三個景點中任意選擇一個游玩,乙從
三個景點中任意選擇一個游玩,乙從![]() 、
、![]() 兩個景點中任意選擇一個游玩.
兩個景點中任意選擇一個游玩.
(1)乙恰好游玩![]() 景點的概率為 ;
景點的概率為 ;
(2)用列表或畫樹狀圖的方法列出所有等可能的結果.并求甲、乙恰好游玩同一景點的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com