
【題目】探究與發(fā)現(xiàn):
探究一:我們知道,三角形的一個外角等于與它不相鄰的兩個內角的和.那么,三角形的一個內角與它不相鄰的兩個外角的和之間存在何種數量關系呢?
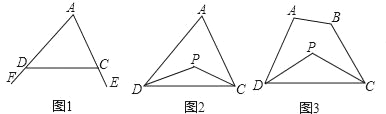
已知:如圖1,∠FDC與∠ECD分別為△ADC的兩個外角,試探究∠A與∠FDC+∠ECD的數量關系.
探究二:三角形的一個內角與另兩個內角的平分線所夾的鈍角之間有何種關系?
已知:如圖2,在△ADC中,DP、CP分別平分∠ADC和∠ACD,試探究∠P與∠A的數量關系.
探究三:若將△ADC改為任意四邊形ABCD呢?
已知:如圖3,在四邊形ABCD中,DP、CP分別平分∠ADC和∠BCD,試利用上述結論探究∠P與∠A+∠B的數量關系.
【答案】探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+![]() ∠A;探究三:∠P=
∠A;探究三:∠P=![]() (∠A+∠B).
(∠A+∠B).
【解析】
探究一:根據三角形的一個外角等于與它不相鄰的兩個內角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根據三角形內角和定理整理即可得解;
探究二:根據角平分線的定義可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根據三角形內角和定理列式整理即可得解;
∠ACD,然后根據三角形內角和定理列式整理即可得解;
探究三:根據四邊形的內角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可.
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分別平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD
∠ACD
=180°﹣![]() (∠ADC+∠ACD)
(∠ADC+∠ACD)
=180°﹣(180°﹣∠A)
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分別平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD
∠BCD
=180°﹣![]() (∠ADC+∠BCD)
(∠ADC+∠BCD)
=180°﹣![]() (360°﹣∠A﹣∠B)
(360°﹣∠A﹣∠B)
=![]() (∠A+∠B).
(∠A+∠B).
故答案為:探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+![]() ∠A;探究三:∠P=
∠A;探究三:∠P=![]() (∠A+∠B).
(∠A+∠B).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個定點坐標分別為A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)請畫出△ABC關于y軸對稱的△A1B1C1;
(2)以原點O為位似中心,將△ABC放大為原來的2倍,得到△A2B2C2 , 畫出△A2B2C2 , 并直接寫出S ![]() :S
:S ![]() = .
= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.動點P從點A出發(fā),沿AB向點B運動,動點Q從點B出發(fā),沿BC向點C運動,如果動點P以2cm/s,Q以1cm/s的速度同時出發(fā),設運動時間為t(s),解答下列問題:
(1)t為______時,△PBQ是等邊三角形?
(2)P,Q在運動過程中,△PBQ的形狀不斷發(fā)生變化,當t為何值時,△PBQ是直角三角形?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系 xOy 中的點 A,給出如下定義:若存在點 B(不與點 A 重合,且直線 AB 不與 坐標軸平行或重合),過點 A 作直線 m∥x 軸,過點 B 作直線 n∥y 軸,直線 m,n 相交于點 C.當線段 AC,BC 的長度相等時,稱點 B 為點 A 的等距點,稱三角形 ABC 的面積為點 A 的等距面積. 例如:如 圖,點 A(2,1),點 B(5,4),因為 AC= BC=3,所以 B 為點 A 的等距點,此時點 A 的等距面積為![]() .
.
(1)點 A 的坐標是(0,1),在點 B1(2,3),B2 (1, 1) , B3 (3, 2) 中,點A的等距點為 .
(2)點 A 的坐標是 (3,1) ,點 A 的等距點 B 在第三象限,
①若點 B 的坐標是 (5, 1) ,求此時點 A 的等距面積;
②若點 A 的等距面積不小于 2,請直接寫出點 B 的橫坐標 t 的取值范圍.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列命題:
①三角形的三條高相交于一點;
②如果一組數據中有一個數據變動,那么它的平均數、眾數、中位數都隨之變動;
③如果不等式![]() 的解集為
的解集為![]() ,那么
,那么![]() ;
;
④如果三角形的一個外角等于與它相鄰的一個內角則這個三角形是直角三角形;
其中正確的命題有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題情境:如圖![]() ,在
,在![]() 中,
中,![]() ,
,![]() 于點D.可知:
于點D.可知:![]() 不需要證明
不需要證明![]() ;
;
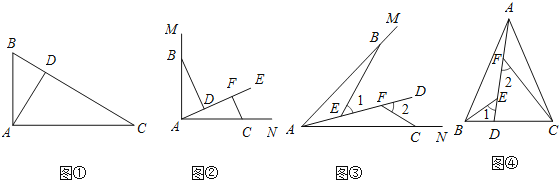
![]() 特例探究:如圖
特例探究:如圖![]() ,
,![]() ,射線AE在這個角的內部,點B、C在
,射線AE在這個角的內部,點B、C在![]() 的邊AM、AN上,且
的邊AM、AN上,且![]() ,
,![]() 于點F,
于點F,![]() 于點
于點![]() 證明:
證明:![]() ≌
≌![]() ;
;
![]() 歸納證明:如圖
歸納證明:如圖![]() ,點B,C在
,點B,C在![]() 的邊AM、AN上,點E,F在
的邊AM、AN上,點E,F在![]() 內部的射線AD上,
內部的射線AD上,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的外角
的外角![]() 已知
已知![]() ,
,![]() 求證:
求證:![]() ≌
≌![]() ;
;
![]() 拓展應用:如圖
拓展應用:如圖![]() ,在
,在![]() 中,
中,![]() ,
,![]() 點D在邊BC上,
點D在邊BC上,![]() ,點E、F在線段AD上,
,點E、F在線段AD上,![]() 若
若![]() 的面積為24,則
的面積為24,則![]() 與
與![]() 的面積之和為______
的面積之和為______![]() 直接寫出結果
直接寫出結果![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在以下說法中:①實數分為正有理數、![]() 、負有理數.②實數和數軸上的點一一對應. ③過直線外一點有且只有一條直線和已知直線垂直.④過一點有且只有一條直線和已知直線 平行.⑤假命題不是命題.⑥如果兩條直線都和第三條直線平行,那么這兩條直線也互相平 行.⑦若一個數的立方根和平方根相同,那么這個數只能是
、負有理數.②實數和數軸上的點一一對應. ③過直線外一點有且只有一條直線和已知直線垂直.④過一點有且只有一條直線和已知直線 平行.⑤假命題不是命題.⑥如果兩條直線都和第三條直線平行,那么這兩條直線也互相平 行.⑦若一個數的立方根和平方根相同,那么這個數只能是![]() . 其中說法正確的個數是( )
. 其中說法正確的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克為標準,超過或不足的分別用正、負來表示,記錄如下:
千克為標準,超過或不足的分別用正、負來表示,記錄如下:
與標準質量的差 |
|
|
|
|
|
|
筐 數 |
|
|
|
|
|
|
(1)與標準質量比較,![]() 筐白菜總計超過或不足多少千克?
筐白菜總計超過或不足多少千克?
(2)若白菜每千克售價![]() 元,則出售這
元,則出售這![]() 筐白菜可賣多少元?
筐白菜可賣多少元?
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com