【題目】在“愛我永州”中學生演講比賽中，五位評委分別給甲、乙兩位選手的評分如下：
甲：8、7、9、8、8
乙：7、9、6、9、9
則下列說法中錯誤的是（ ）
A.甲、乙得分的平均數都是8
B.甲得分的眾數是8，乙得分的眾數是9
C.甲得分的中位數是9，乙得分的中位數是6
D.甲得分的方差比乙得分的方差小
【答案】C
【解析】解：A、 
= 
=8， 
= 
=8，故此選項正確；
B、甲得分次數最多是8分，即眾數為8分，乙得分最多的是9分，即眾數為9分，故此選項正確；
C、∵甲得分從小到大排列為：7、8、8、8、9，∴甲的中位數是8分；
∵乙得分從小到大排列為：6、7、9、9、9，∴乙的中位數是9分；故此選項錯誤；
D、∵ 
= 
×[（8﹣8）2+（7﹣8）2+（9﹣8）2+（8﹣8）2+（8﹣8）2]= ×2=0.4，
= ×[（7﹣8）2+（9﹣8）2+（6﹣8）2+（9﹣8）2+（9﹣8）2]= ×8=1.6，∴ ＜ ，故D正確；
故選：C．
分別求出甲、乙的平均數、眾數、中位數及方差可逐一判斷．本題主要考查平均數、眾數、中位數及方差，熟練掌握這些統計量的意義及計算公式是解題的關鍵．
閱讀快車系列答案科目：初中數學 來源： 題型：
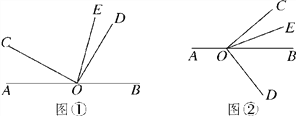
【題目】已知O是直線AB上的一點，∠COD是直角，OE平分∠BOC.
（1）如圖①，若∠AOC＝30°，求∠DOE的度數；
（2）在圖①中，若∠AOC＝
，直接寫出∠DOE的度數（用含
的代數式表示）；
（3）將圖①中的∠DOC繞頂點O順時針旋轉至圖②的位置，探究∠AOC和∠DOE的度數之間的關系，寫出你的結論，并說明理由；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若十位上的數字比個位上的數字、百位上的數字都大的三位數叫做中高數，如796就是一個“中高數”．若一個三位數的十位上數字為7，且從4、5、6、8中隨機選取兩數，與7組成“中高數”，那么組成“中高數”的概率是多少？（請用“畫樹狀圖”或“列表”等方法寫出分析過程）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】A、B兩地相距70千米，甲從A地出發，每小時行15千米，乙從B地出發，每小時行20千米．
（1）若兩人同時出發，相向而行，則經過幾小時兩人相遇？
（2）若甲在前，乙在后，兩人同時同向而行，則幾小時后乙追上甲？
（3）若兩人同時出發，相向而行，則幾小時后兩人相距10千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某檢修小組乘汽車從
地出發，在東西走向的馬路上檢修線路，如果規定向東行駛為正，一天中七個檢修點的行駛記錄如下（單位：
）：
－4，＋7，－9，＋8，＋6，－4，－3．
（1）收工時汽車共行駛了多少千米？
（2）收工時，汽車距地多遠？
（3）在檢修時，第幾個檢修點離地最遠，最遠距離是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，∠DAC是△ABC的一個外角．
實驗與操作：根據要求進行尺規作圖，并在圖中標明相應字母（保留作圖痕跡，不寫作法）
（1）作∠DAC的平分線AM；
（2）作線段AC的垂直平分線，與AM交于點F，與BC邊交于點E，連接AE、CF
探究與猜想：若∠BAE=36°，求∠B的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，在下列各圖中，點O為直線AB上一點，∠AOC＝60°，直角三角板的直角頂點放在點處．
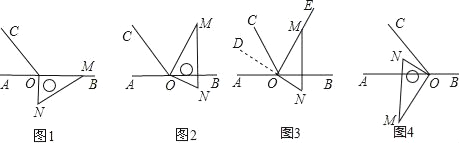
（1）如圖1，三角板一邊OM在射線OB上，另一邊ON在直線AB的下方，則∠BOC的度數為 °，∠CON的度數為 °；
（2）如圖2，三角板一邊OM恰好在∠BOC的角平分線OE上，另一邊ON在直線AB的下方，此時∠BON的度數為 °；
（3）請從下列（A），（B）兩題中任選一題作答．
我選擇： ．
（A）在圖2中，延長線段NO得到射線OD，如圖3，則∠AOD的度數為 °；∠DOC與∠BON的數量關系是∠DOC ∠BON（填“＞”、“＝”或“＜”）；
（B）如圖4，MN⊥AB，ON在∠AOC的內部，若另一邊OM在直線AB的下方，則∠COM+∠AON的度數為 °；∠AOM﹣∠CON的度數為 °．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀后解決問題：
在“15.3分式方程”一課的學習中，老師提出這樣的一個問題：如果關于x的分式方程
的解為正數，那么a的取值范圍是什么？
經過交流后，形成下面兩種不同的答案：
小明說：解這個關于x的分式方程，得到方程的解為x=a﹣2．
因為解是正數，可得a﹣2＞0，所以a＞2．
小強說：本題還要必須a≠3，所以a取值范圍是a＞2且a≠3．
（1）小明與小強誰說的對，為什么？
（2）關于x的方程
有整數解，求整數m的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
