
 如圖,某天晚8點時,一臺風中心位于點O正北方向160千米點A處,臺風中心以每小時20千米的速度向東南方向移動,在距臺風中心小于等于120千米的范圍內將受到臺風影響,同時在點O有一輛汽車以每小時40千米的速度向東行駛.
如圖,某天晚8點時,一臺風中心位于點O正北方向160千米點A處,臺風中心以每小時20千米的速度向東南方向移動,在距臺風中心小于等于120千米的范圍內將受到臺風影響,同時在點O有一輛汽車以每小時40千米的速度向東行駛.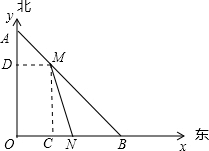
 AM=10
AM=10 t,
t, t,160-10
t,160-10 t),
t), t)2+(160-10
t)2+(160-10 t)2=1202,
t)2=1202, )t2-32
)t2-32 t+112=0,
t+112=0, -6912<0,
-6912<0,

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com