
【題目】邊長為10、10、12的三角形的外接圓半徑為R,內切圓半徑為r,則R+r=_____.
【答案】![]() .
.
【解析】
根據等腰三角形的性質得出內心和外心都在底邊的高AD上,根據勾股定理得出方程,即可求出外接圓的半徑,根據三角形的面積公式即可求出內切圓的半徑.
解:如圖1,
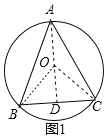
∵在△ABC中,AB=AC=10,BC=12,
∴過A作AD⊥BC于D,則外接圓的圓心O在AD上,連接OB、OC,
∴BD=CD=![]() BC=6,
BC=6,
∴AD=![]() =8,
=8,
∵OB2=OD2+BD2,
∴R2=(8﹣R)2+36
∴R=![]()
如圖2
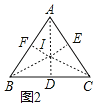
過A作AD⊥BC于D,
∵△ABC中,AB=AC,
∴△ABC的內心I在AD上,過I作IE⊥AC于E,IF⊥AB于F,連接OA、OB、OC,
則IF=IE=ID=r,
∵S△ABC=S△BIC+S△AIC+S△ABI,
∴![]() ×12×8=
×12×8=![]() ×12×r+
×12×r+![]() ×10×r+
×10×r+![]() ×10×r
×10×r
∴r=3
∴R+r=![]() +3=
+3=![]()
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖①,已知拋物線![]() 的頂點為點P,與y軸交于點B.點A坐標為(3,2).點M為拋物線上一動點,以點M為圓心,MA為半徑的圓交x軸于C,D兩點(點C在點D的左側).
的頂點為點P,與y軸交于點B.點A坐標為(3,2).點M為拋物線上一動點,以點M為圓心,MA為半徑的圓交x軸于C,D兩點(點C在點D的左側).

(1)如圖②,當點M與點B重合時,求CD的長;
(2)當點M在拋物線上運動時,CD的長度是否發生變化?若變化,求出CD關于點M橫坐標x的函數關系式;若不發生變化,求出CD的長;
(3)當△ACP與△ADP相似時,求出點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解題:學習了二次根式后,你會發現一些含有根號的式子可以寫成另一個式子的平方,如3+2![]() =(1+
=(1+![]() )2,我們來進行以下的探索:
)2,我們來進行以下的探索:
設a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n都是正整數),則有a+b
)2(其中a,b,m,n都是正整數),則有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,這樣就得出了把類似a+b
,∴a=m2+2n2,b=2mn,這樣就得出了把類似a+b![]() 的式子化為平方式的方法,請仿照上述方法探索并解決下列問題:
的式子化為平方式的方法,請仿照上述方法探索并解決下列問題:
(1)當a,b,m,n都為正整數時,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分別表示a,b,得a= ,b= .
)2,用含m,n的式子分別表示a,b,得a= ,b= .
(2)若a﹣4![]() =(m﹣n
=(m﹣n![]() )2且a,m,n都為正整數,求a的值.
)2且a,m,n都為正整數,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,是由北京國際數學家大會的會徽演化而成的圖案,其主體部分是由一連串的等腰直角三角形依次連接而成,其中∠MA1A2=∠MA2A3…=∠MAnAn+1=90°,(n為正整數),若M點的坐標是(﹣1,2),A1的坐標是(0,2),則A22的坐標為( )

A.(﹣1﹣29,2﹣29)B.(1﹣29,2﹣29)
C.(﹣1﹣210,2﹣210)D.(1﹣210,2﹣210)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形ABC內接于⊙O,CA=CB,過點A作AE∥BC,交⊙O于點E,過點C作⊙O的切線交AE的延長線于點D,已知AB=6,BE=3![]() .
.
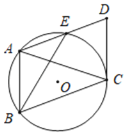
(1)求證:四邊形ABCD為平行四邊形;
(2)延長AO交DC的延長線于點F,求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A城有某種農機30臺,B城有該農機40臺.現要將這些農機全部運往C、D兩鄉,調運任務承包給某運輸公司.已知C鄉需要農機34臺,D鄉需要農機36臺,從A城往C、D兩鄉運送農機的費用分別為250元/臺和200元/臺,從B城往C、D兩鄉運送農機的費用分別為150元/臺和240元/臺
(1)設A城運往C鄉該農機x臺,運送全部農機的總費用為W元,求W關于x的函數關系式,并直接寫出自變量x的取值范圍;
(2)現該運輸公司要求運送全部農機的總費用不低于16460元,則有多少種不同的調運方案?將這些方案設計出來;
(3)現該運輸公司決定對A城運往C鄉的農機,從運輸費中每臺減免a元(100<a<250)作為優惠,其他費用不變.在(2)的條件下,若總費用最小值為10740元,直接寫出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場要經營一種新上市的文具,進價為20元,試營銷階段發現:當銷售單價是25元時,每天的銷售量為250件,銷售單價每上漲1元,每天的銷售量就減少10件
(1)寫出商場銷售這種文具,每天所得的銷售利潤![]() (元)與銷售單價
(元)與銷售單價![]() (元)之間的函數關系式;
(元)之間的函數關系式;
(2)求銷售單價為多少元時,該文具每天的銷售利潤最大;
(3)商場的營銷部結合上述情況,提出了A、B兩種營銷方案
方案A:該文具的銷售單價高于進價且不超過30元;
方案B:每天銷售量不少于10件,且每件文具的利潤至少為25元
請比較哪種方案的最大利潤更高,并說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若二次函數y=ax2+bx+c(a≠0)圖象的對稱軸為x=1,與y軸交于點C,與x軸交于點A、點B(﹣1,0),則
①二次函數的最大值為a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④當y>0時,﹣1<x<3,其中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一次函數y=-x+6的圖象上取一點P,作PA⊥x軸于點A,PB⊥y軸于點B,且矩形PBOA的面積為5,則在x軸上方滿足上述條件的點P是( )
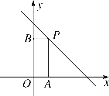
A.(1,5)、(5,1)
B.(1,5)、(5,1)、(3+![]() ,3-
,3-![]() )、(3-
)、(3-![]() ,3+
,3+![]() )
)
C.(1,5)、(5,1)、(3-![]() ,3+
,3+![]() )
)
D.(1,5)、(2+![]() ,2-
,2-![]() )、(2-
)、(2-![]() ,2+
,2+![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com