
【題目】如圖,在矩形![]() 中,對角線
中,對角線![]() 、
、![]() 交于點
交于點![]() ,將
,將![]() 沿直線
沿直線![]() 翻折,點
翻折,點![]() 落在點
落在點![]() 處,且
處,且![]() ,連接
,連接![]() .求證:
.求證:
(![]() )
)![]() 是等邊三角形.
是等邊三角形.
(![]() )
)![]() .
.
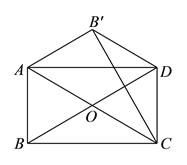
【答案】(1)證明見解析;(2)證明見解析.
【解析】試題分析:(1)由四邊形ABCD是矩形,得到∠BAD=90°,AO=OD,得到∠OAD=∠ADO,根據平行線的性質得到∠B′AD=∠ADB,等量代換得到∠B′AD=∠DAC,根據折疊的性質得到∠BAC=∠CAB′,得到∠DAC=![]() ∠BAC,求得∠BAC=60°,于是得到結論;(2)連接B′O,推出B′C垂直平分OD,得到B′O=B′D,根據等腰三角形的性質得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到結論.
∠BAC,求得∠BAC=60°,于是得到結論;(2)連接B′O,推出B′C垂直平分OD,得到B′O=B′D,根據等腰三角形的性質得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到結論.
試題解析:( ![]() )∵四邊形
)∵四邊形![]() 是矩形,
是矩形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 是由
是由![]() 沿直線
沿直線![]() 翻折得到,
翻折得到,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 是等邊三角形.
是等邊三角形.
(![]() )∵
)∵![]() 是由
是由![]() 沿直線
沿直線![]() 翻折得到,
翻折得到,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】甲、乙兩地相距135千米,大小兩輛汽車從甲地開往乙地,大汽車比小汽車早出發4小時,小汽車比大汽車早到30分鐘,小汽車和大汽車的速度之比為5∶2,求兩車的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初三(1)班要從甲、乙、丙、丁這![]() 名同學中隨機選取
名同學中隨機選取![]() 名同學參加學校畢業生代表座談會.求下列事件的概率:
名同學參加學校畢業生代表座談會.求下列事件的概率:
(![]() )已確定甲參加,另外
)已確定甲參加,另外![]() 人恰好選中乙;
人恰好選中乙;
(![]() )隨機選取
)隨機選取![]() 名同學,恰好選中甲和乙.
名同學,恰好選中甲和乙.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小敏進行賽跑訓練,他們選擇了一個土坡,按同一路線同時出發,從坡腳跑到坡頂再原路返回坡腳.他們倆上坡的平均速度不同,下坡的平均速度則是各自上坡平均速度的![]() 倍.設兩人出發
倍.設兩人出發![]() 后距出發點的距離為ym.圖中折線段
后距出發點的距離為ym.圖中折線段![]() 表示小明在整個訓練中y與x的函數關系.
表示小明在整個訓練中y與x的函數關系.
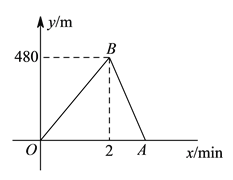
(![]() )點
)點![]() 所表示的實際意義是__________.
所表示的實際意義是__________.
(![]() )求
)求![]() 所在直線的函數表達式.
所在直線的函數表達式.
(![]() )如果小敏上坡平均速度是小明上坡平均速度的一半,那么兩人出發后多長時間第一次相遇?
)如果小敏上坡平均速度是小明上坡平均速度的一半,那么兩人出發后多長時間第一次相遇?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com