
【題目】如圖,AD為△ABC的高,BE為△ABC的角平分線,若∠EBA=34°,∠AEB=72°.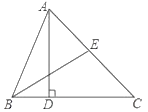
(1)求∠CAD和∠BAD的度數;
(2)若點F為線段BC上任意一點,當△EFC為直角三角形時,試求∠BEF的度數.
【答案】
(1)解:∵BE為△ABC的角平分線,
∴∠CBE=∠EBA=34°,
∵∠AEB=∠CBE+∠C,
∴∠C=72°﹣34°=38°,
∵AD為△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=52°,
∠BAD=90°-∠ABD=90°-68°=22°
(2)解:當∠EFC=90°時,∠BEF=90°﹣∠CBE=56°,
當∠FEC=90°時,∠BEF=180°-72°﹣90°=18°
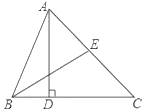
【解析】(1)由BE為∠ABC的平分線,得出∠BAD=22°,再求出∠C,得出∠CAD=52°,即可得出結論;
(2)分兩種情況:①當∠EFC=90°時;②當∠FEC=90°時;由角的互余關系和三角形的外角性質即可求出∠BEF的度數.
【考點精析】認真審題,首先需要了解角的平分線(從一個角的頂點引出的一條射線,把這個角分成兩個相等的角,這條射線叫做這個角的平分線),還要掌握垂線的性質(垂線的性質:1、過一點有且只有一條直線與己知直線垂直.2、垂線段最短)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】某人要在規定的時間內加工100個零件,則工作效率η與時間t之間的關系中,下列說法正確的是( )
A.數100和η,t都是變量
B.數100和η都是常量
C.η和t是變量
D.數100和t都是常量
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖線段AB=9,C、D、E分別為線段AB(端點A、B除外)上順次三個不同的點,圖中所有的線段和等于46,則下列結論一定成立的是( ) ![]()
A.CD=3
B.DE=2
C.CE=5
D.EB=5
查看答案和解析>>
科目:初中數學 來源: 題型:
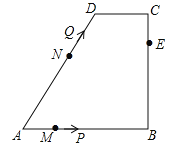
【題目】如圖,在四邊形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分別是AB、AD、CB上的點,AM=CE=1,AN=3,點P從點M出發,以每秒1個單位長度的速度沿折線MB﹣BE向點E運動,同時點Q從點N出發,以相同的速度沿折線ND﹣DC﹣CE向點E運動,當其中一個點到達后,另一個點也停止運動.設△APQ的面積為S,運動時間為t秒,則S與t函數關系的大致圖象為( )
A.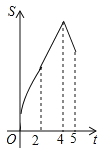 B.
B.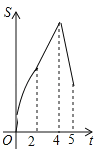 C.
C.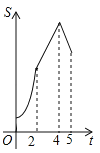 D.
D.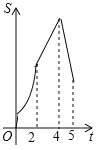
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com