
 個單位勻速運動,同時點Q從點D(0,2)出發,沿y軸正方
個單位勻速運動,同時點Q從點D(0,2)出發,沿y軸正方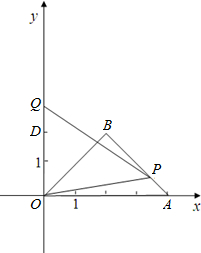 向以每秒2個單位勻速運動,當點P到達點O時,兩點同時停止運動,設運動的時間為t秒.
向以每秒2個單位勻速運動,當點P到達點O時,兩點同時停止運動,設運動的時間為t秒. 解:(1)過B作BE⊥OA于E
解:(1)過B作BE⊥OA于E

 t由勾股定理得
t由勾股定理得 (4-t)(2+2t)
(4-t)(2+2t)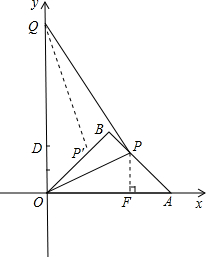
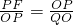
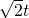 ,∴PF=AF=t,OQ=2+2t
,∴PF=AF=t,OQ=2+2t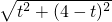





 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
| 2 |
 向以每秒2個單位勻速運動,當點P到達點O時,兩點同時停止運動,設運動的時間為t秒.
向以每秒2個單位勻速運動,當點P到達點O時,兩點同時停止運動,設運動的時間為t秒.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•河北)如圖,△OAB中,OA=OB=10,∠AOB=80°,以點O為圓心,6為半徑的優弧
(2013•河北)如圖,△OAB中,OA=OB=10,∠AOB=80°,以點O為圓心,6為半徑的優弧 |
| MN |
 |
| MN |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2008年浙江省溫州市實驗中學中考數學一模試卷(解析版) 題型:解答題
 個單位勻速運動,同時點Q從點D(0,2)出發,沿y軸正方向以每秒2個單位勻速運動,當點P到達點O時,兩點同時停止運動,設運動的時間為t秒.
個單位勻速運動,同時點Q從點D(0,2)出發,沿y軸正方向以每秒2個單位勻速運動,當點P到達點O時,兩點同時停止運動,設運動的時間為t秒.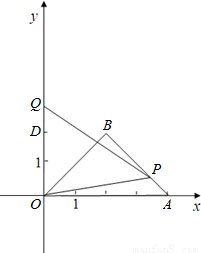
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com