
【題目】在一次課題學習活動中,老師提出了如下問題:如圖,四邊形![]() 是正方形,點
是正方形,點![]() 是邊
是邊![]() 的中點,
的中點,![]() ,且
,且![]() 交正方形外角平分線
交正方形外角平分線![]() 于點
于點![]() .請你探究
.請你探究![]() 與
與![]() 存在怎樣的數量關系,并證明你的結論正確.經過探究,小明得出的結論是
存在怎樣的數量關系,并證明你的結論正確.經過探究,小明得出的結論是![]() ,而要證明結論
,而要證明結論![]() ,就需要證明
,就需要證明![]() 和
和![]() 所在的兩個三角形全等,但
所在的兩個三角形全等,但![]() 和
和![]() 顯然不全等(一個是直角三角形,一個是鈍角三角形),考慮到點
顯然不全等(一個是直角三角形,一個是鈍角三角形),考慮到點![]() 是邊
是邊![]() 的中點,小明想到的方法是如圖2,取
的中點,小明想到的方法是如圖2,取![]() 的中點
的中點![]() ,連接
,連接![]() ,證明
,證明![]() .從而得到
.從而得到![]() .請你參考小明的方法解決下列問題.
.請你參考小明的方法解決下列問題.
(1)如圖3,若把條件“點![]() 是邊
是邊![]() 的中點”改為“點
的中點”改為“點![]() 是邊
是邊![]() 上的任意一點”,其余條件不變,證明結論
上的任意一點”,其余條件不變,證明結論![]() 仍然成立;
仍然成立;
(2)如圖4,若把條件“點![]() 是邊
是邊![]() 的中點”改為:“點
的中點”改為:“點![]() 是邊
是邊![]() 延長線上的一點”,其余條件仍不變,那么結論
延長線上的一點”,其余條件仍不變,那么結論![]() 是否還成立?若成立,請完成證明過程,若不成立,請說明理由.
是否還成立?若成立,請完成證明過程,若不成立,請說明理由.




【答案】(1)正確,見解析;(2)正確,見解析
【解析】
(1)在AB上取點![]() ,連接
,連接![]() ,證明△PAE≌△CEF即可;
,證明△PAE≌△CEF即可;
(2)延長BA至![]() ,使
,使![]() =CE,連接
=CE,連接![]() ,證明△ANE≌△ECF即可.
,證明△ANE≌△ECF即可.
解:(1)正確.
證明:在AB上取一點M,使AM=EC,連接ME.
![]() 四邊形
四邊形![]() 是正方形,
是正方形,
![]()
∴BM=BE,
∴∠BME=45°,
∴∠AME=135°,
∵CF是外角平分線,
∴∠DCF=45°,
∴∠ECF=135°,
∴∠AME=∠ECF,
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴△AME≌△ECF(ASA),
∴AE=EF.
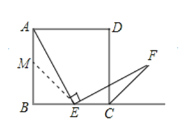
(2)正確.
證明:在BA的延長線上取一點N.
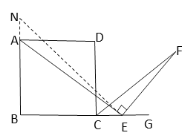
使AN=CE,連接NE.
∴BN=BE,
∴∠N=∠NEC=45°,
∵CF平分∠DCG,
∴∠FCE=45°,
∴∠N=∠ECF,
∵四邊形ABCD是正方形,
∴AD∥BE,
∴∠DAE=∠BEA,
即∠DAE+90°=∠BEA+90°,
∴∠NAE=∠CEF,
∴△ANE≌△ECF(ASA)
∴AE=EF.


科目:初中數學 來源: 題型:
【題目】某種流感病毒,有一人患了這種流感,在每輪傳染中一人將平均傳給x人.
(1)求第一輪后患病的人數;(用含x的代數式表示)
(2)在進入第二輪傳染之前,有兩位患者被及時隔離并治愈,問第二輪傳染后總共是否會有21人患病的情況發生,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD與AC相交于點E,AB=9,BC=4,DC=3.
(1)求BE的長度;
(2)求△ABE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在美化校園的活動中,某興趣小組想借助如圖所示的直角墻角(兩邊足夠長),用28m長的籬笆圍成一個矩形花園ABCD(籬笆只圍AB,BC兩邊),設AB=xm.

(1)若花園的面積為192m2,求x的值;
(2)若在P處有一棵樹與墻CD,AD的距離分別是15m和6m,要將這棵樹圍在花園內(含邊界,不考慮樹的粗細),求x取何值時,花園面積S最大,并求出花園面積S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
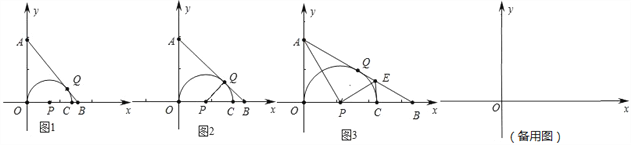
【題目】平面直角坐標系中,A(0,4),點P從原點O開始向x軸正方向運動,設P點橫坐標為m,以點P為圓心,PO為半徑作⊙P交x 軸另一點為C,過點A作⊙P的切線交 x軸于點B,切點為Q.
(1)如圖1,當B點坐標為(3,0)時,求m;
(2)如圖2,當△PQB為等腰三角形時,求m;
(3)如圖3,連接AP,作PE⊥AP交AB于點E,連接CE,求證:CE是⊙P的切線;
(4)若在x軸上存在點M(8,0),在點P整個運動過程中,求MQ的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學習小組發現一個結論:已知直線a∥b,若直線c∥a,則c∥b.他們發現這個結論運用很廣,請你利用這個結論解決以下問題:

已知直線AB∥CD,點E在AB、CD之間,點P、Q分別在直線AB、CD上,連接PE、EQ.
(1)如圖1,運用上述結論,探究∠PEQ與∠APE+∠CQE之間的數量關系,并說明理由;
(2)如圖2,PF平分∠BPE,QF平分∠EQD,當∠PEQ=140°時,求出∠PFQ的度數;
(3)如圖3,若點E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延長線交PF于點F.當∠PEQ=70°時,請求出∠PFQ的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于點D,DE⊥AB,垂足為E。若DE=1,則BC的長為( )

A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,對角線
中,對角線![]() 交于點
交于點![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.下列結論正確的是( )
的中點.下列結論正確的是( )
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() ;⑤四邊形
;⑤四邊形![]() 是菱形.
是菱形.
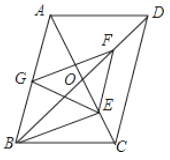
A.③⑤B.①②④C.①②③④D.①②③④⑤
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com