
【題目】平面直角坐標系中有兩點![]() 、
、![]() ,我們定義
,我們定義![]() 、
、![]() 兩點間的“
兩點間的“![]() 值”直角距離為
值”直角距離為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() .小靜和佳佳在解決問題:(求點
.小靜和佳佳在解決問題:(求點![]() 與點
與點![]() 的“1值”直角距離
的“1值”直角距離![]() )時,采用了兩種不同的方法:
)時,采用了兩種不同的方法:
(方法一):![]() ;
;
(方法二):如圖1,過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作直線
作直線![]() 與
與![]() 軸交于點
軸交于點![]() ,則
,則![]()
請你參照以上兩種方法,解決下列問題:
(1)已知點![]() ,點
,點![]() ,則
,則![]() 、
、![]() 兩點間的“2值”直角距離
兩點間的“2值”直角距離![]() .
.
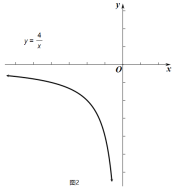
(2)函數![]() 的圖像如圖2所示,點
的圖像如圖2所示,點![]() 為其圖像上一動點,滿足
為其圖像上一動點,滿足![]() 兩點間的“
兩點間的“![]() 值”直角距離
值”直角距離![]() ,且符合條件的點
,且符合條件的點![]() 有且僅有一個,求出符合條件的“
有且僅有一個,求出符合條件的“![]() 值”和點
值”和點![]() 坐標.
坐標.
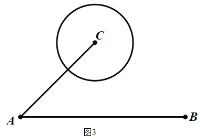
(3)城市的許多街道是相互垂直或平行的,因此,往往不能沿直線行走到達目的地,只能按直角拐彎的方式行走,因此,兩地之間修建垂直和平行的街道常常轉化為兩點間的“![]() 值”直角距離,
值”直角距離,![]() 地位于
地位于![]() 地的正東方向上,
地的正東方向上,![]() 地在
地在![]() 點東北方向上且相距
點東北方向上且相距![]() ,以
,以![]() 為圓心修建了一個半徑為
為圓心修建了一個半徑為![]() 的圓形濕地公園,現在要在公園和
的圓形濕地公園,現在要在公園和![]() 地之間修建觀光步道.步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元,問:修建這一規光步道至少要多少萬元?
地之間修建觀光步道.步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元,問:修建這一規光步道至少要多少萬元?

【答案】(1)10 (2)![]() ,
,![]() (3)
(3)![]()
【解析】
(1)根據直角距離的公式,直接代入求解即可;
(2)設點C的坐標為![]() ,代入直角距離公式可得
,代入直角距離公式可得![]() 根據根的判別式求出k的值,即可求出點C的坐標;
根據根的判別式求出k的值,即可求出點C的坐標;
(3)如圖,⊙C與線段AC交于點D,過點D作![]() 與AB交于點E,先證明△ADE是等腰直角三角形,從而得出
與AB交于點E,先證明△ADE是等腰直角三角形,從而得出![]() ,再根據直角距離的定義,即可求出出最低的成本.
,再根據直角距離的定義,即可求出出最低的成本.
(1)∵![]() ,點
,點![]() ,點
,點![]()
∴![]() ;
;
(2)設點C的坐標為![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵符合條件的點![]() 有且僅有一個,且
有且僅有一個,且![]()
∴![]()
解得![]()
∴![]()
![]()
![]()
解得![]()
∴![]()
故![]() ,
,![]() ;
;
(3)如圖,⊙C與線段AC交于點D,過點D作![]() 與AB交于點E
與AB交于點E
由題意得![]()
∴![]()
∵![]()
∴△ADE是等腰直角三角形
∴![]()
∵步道只能東西或者南北走向,并且東西方向每千米成本是20萬元,南北方向每千米的成本是10萬元
∴步道的最短距離為A和D的直角距離,即![]()
最低總成本![]() (萬元)
(萬元)
故修建這一規光步道至少要![]() 萬元.
萬元.


科目:初中數學 來源: 題型:
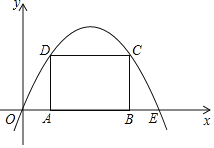
【題目】如圖,拋物線y=ax2+bx(a<0)過點E(10,0),矩形ABCD的邊AB在線段OE上(點A在點B的左邊),點C,D在拋物線上.設A(t,0),當t=2時,AD=4.
(1)求拋物線的函數表達式.
(2)當t為何值時,矩形ABCD的周長有最大值?最大值是多少?
(3)保持t=2時的矩形ABCD不動,向右平移拋物線.當平移后的拋物線與矩形的邊有兩個交點G,H,且直線GH平分矩形的面積時,求拋物線平移的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
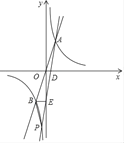
【題目】如圖,過原點O的直線與雙曲線y=![]() 交于上A(m,n)、B,過點A的直線交x軸正半軸于點D,交y軸負半軸于點E,交雙曲線y=
交于上A(m,n)、B,過點A的直線交x軸正半軸于點D,交y軸負半軸于點E,交雙曲線y=![]() 于點P.
于點P.
(1)當m=2時,求n的值;
(2)當OD:OE=1:2,且m=3時,求點P的坐標;
(3)若AD=DE,連接BE,BP,求△PBE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著信息技術的快速發展,“互聯網+”滲透到我們日常生活的各個領域,網上在線學習交流已不再是夢,現有某教學網站策劃了A,B兩種上網學習的月收費方式:
收費方式 | 月使用費/元 | 包時上網時間/h | 超時費/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
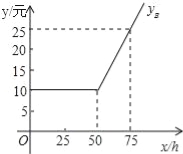
設每月上網學習時間為x小時,方案A,B的收費金額分別為yA,yB.
(1)如圖是yB與x之間函數關系的圖象,請根據圖象填空:m= ;n=
(2)寫出yA與x之間的函數關系式.
(3)選擇哪種方式上網學習合算,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車從A地出發,沿同一路線駛向B地.甲車先出發勻速駛向B地,40min后,乙車出發,勻速行駛一段時間后,在途中的貨站裝貨耗時半小時.由于滿載貨物,為了行駛安全,速度減少了50km/h,結果與甲車同時到達B地,甲乙兩車距A地的路程![]() (
(![]() )與乙車行駛時間
)與乙車行駛時間![]() (
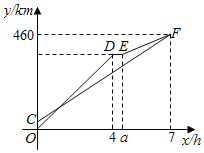
(![]() )之間的函數圖象如圖所示,則下列說法:①
)之間的函數圖象如圖所示,則下列說法:①![]() ②甲的速度是60km/h;③乙出發80min追上甲;④乙車在貨站裝好貨準備離開時,甲車距B地150km;⑤當甲乙兩車相距30 km時,甲的行駛時間為1 h、3 h、
②甲的速度是60km/h;③乙出發80min追上甲;④乙車在貨站裝好貨準備離開時,甲車距B地150km;⑤當甲乙兩車相距30 km時,甲的行駛時間為1 h、3 h、![]() h;其中正確的是__________.
h;其中正確的是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
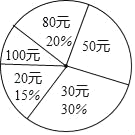
【題目】在“全民讀書月”活動中,小明調查了班級里40名同學本學期購買課外書的費用情況,并將結果繪制成如圖所示的統計表和扇形統計圖,請根據相關信息,解答下列問題:(直接填寫結果)
費用(元) | 20 | 30 | 50 | 80 | 100 |
人數 | 6 | a | 10 | b | 4 |
(1)本次調查獲取的樣本數據的眾數是 元,中位數是 元;
(2)扇形統計圖中,“50元”所對應的圓心角的度數為 度,該班學生購買課外書的平均費用為 元;
(3)若該校共有學生1000人,根據樣本數據,估計本學期購買課外書花費50元的學生有 人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點△ABC(頂點是網格線的交點)和點A1.
(1)畫出一個格點△A1B1C1,并使之是由△ABC平移后得到,且A與A1是對應點;
(2)畫出點B關于直線AC的對稱點D,并指出AD可以看作由AB繞A點經過怎樣的旋轉而得的;
(3)將△ABC繞點A逆時針旋轉一定角度,使得AB落在(2)中的線段AD的位置,請作出旋轉后的三角形,并求在這一旋轉過程中△ABC掃過的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數 y=kx-2 的圖象與 x 軸、y 軸分別交于 A,B 兩點,與反比例函數![]() 的圖象交于點 C,且 AB=AC,則 k 的值為( )
的圖象交于點 C,且 AB=AC,則 k 的值為( )
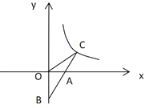
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形![]() 是正方形,
是正方形,![]() 是等邊三角形,
是等邊三角形,![]() 為對角線
為對角線![]() (不含
(不含![]() 點)上任意一點,將
點)上任意一點,將![]() 繞點
繞點![]() 逆時針旋轉60°得到
逆時針旋轉60°得到![]() ,連接
,連接![]() 、
、![]() 、
、![]() .
.
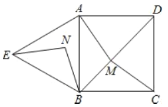
(1)求證![]() ;
;
(2)①當![]() 點在何處時,
點在何處時,![]() 的值最小;
的值最小;
②當![]() 點在何處時,
點在何處時,![]() 的值最小,并說明理由;
的值最小,并說明理由;
(3)當![]() 的最小值為
的最小值為![]() 時,求正方形的邊長.
時,求正方形的邊長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com