【題目】如圖，拋物線y=ax2+bx+3與x軸相交于點A（﹣3，0），B（﹣1，0），與y軸相交于點C，⊙O1為△ABC的外接圓，交拋物線于另一點D．
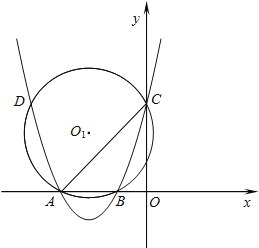
（1）求拋物線的解析式；
（2）求⊙O1的半徑．
【答案】（1）y=x2+4x+3；（2）
．
【解析】
試題分析：（1）利用待定系數法求出拋物線的解析式；
（2）如圖所示，由圓周角定理，確定△BO1C為等腰直角三角形，從而求出半徑的長度．
解：（1）∵拋物線y=ax2+bx+3與x軸相交于點A（﹣3，0），B（﹣1，0），
∴
，
解得a=1，b=4，
∴拋物線的解析式為：y=x2+4x+3；
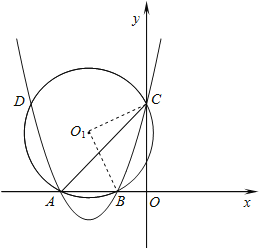
（2）由（1）知，拋物線解析式為：y=x2+4x+3，
∵令x=0，得y=3，
∴C（0，3），
∴OC=OA=3，則△AOC為等腰直角三角形，
∴∠CAB=45°，
在Rt△BOC中，由勾股定理得：BC=
=
，
如圖1所示，連接O1B、O1B，
由圓周角定理得：∠BO1C=2∠BAC=90°，
∴△BO1C為等腰直角三角形，
∴⊙O1的半徑O1B=
BC=．
考前必練系列答案科目：初中數學 來源： 題型：
【題目】如圖，在教學實踐課中，小明為了測量學校旗桿CD的高度，在地面A處放置高度為1.5米的測角儀AB，測得旗桿頂端D的仰角為32°，AC=22米，求旗桿CD的高度．（結果精確到0.1米．參考數據：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將△ABC繞著點C順時針旋轉50°后得到△A′B′C′．若∠A=40°．∠B′=110°，則∠BCA′的度數是（ ）
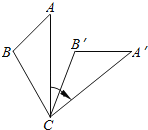
A．110° B．80° C．40° D．30°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列命題正確的是（ ）
A．若兩弦相等，則它們所對的弧相等
B．若弦長等于半徑，則弦所對的劣弧的度數為60°
C．若兩弧不等，則大弧所對的圓心角較大
D．若兩弧的度數相等，則兩條弧是等弧
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知如圖，菱形ABCD的四個頂點均在坐標軸上，對角線AC、BD交于原點O，DF⊥AB交AC于點G，反比例函數y=
（x＞0）經過線段DC的中點E，若BD=4，則AG的長為（ ）
A．
B．
+2 C．2+1 D．
+1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com