
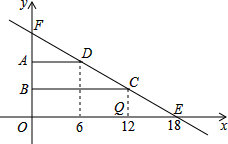
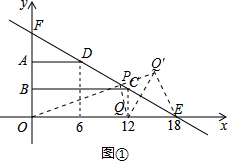
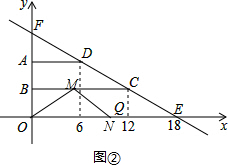
 已知直角梯形ABCD如圖放置在平面直角坐標系中,∠DCB=30°,AB邊在y軸上,點D的橫坐標為6,CQ⊥x軸,垂足為Q,點Q的橫坐標為12,過CD的直線l交x軸于點E,E點坐標為(18,0).
已知直角梯形ABCD如圖放置在平面直角坐標系中,∠DCB=30°,AB邊在y軸上,點D的橫坐標為6,CQ⊥x軸,垂足為Q,點Q的橫坐標為12,過CD的直線l交x軸于點E,E點坐標為(18,0).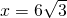 ,
,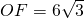 ,則F(0,
,則F(0, ),
), )兩點,
)兩點,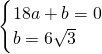 ,
,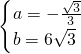 ,
,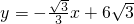 ,
, ;當x=12時,y=
;當x=12時,y= ,
, ),B(0,
),B(0, ).
).
 ),
),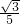 x,
x, ,
,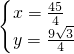 ,
, ,
, ),
),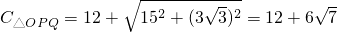 .
.
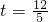 s,
s,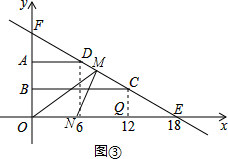
 ,所以6<t≤6+
,所以6<t≤6+ ,而此時點N已經向左運動超過了點(6,0),
,而此時點N已經向左運動超過了點(6,0), <t<12,(注意,點N先到達終點,因而只能運動12秒就停止了).
<t<12,(注意,點N先到達終點,因而只能運動12秒就停止了). -2t,ON=12-t,
-2t,ON=12-t,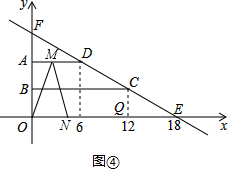
 -2t)=12-t,
-2t)=12-t,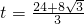 >12s,所以在DA上不可能存在點M.
>12s,所以在DA上不可能存在點M.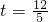 s或t=12s時MO=MN.
s或t=12s時MO=MN.

 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
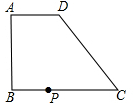 PD中邊AP上的高為( )
PD中邊AP上的高為( )A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
 結論是否成立?請說明理由.
結論是否成立?請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
 已知直角梯形ABCD如圖放置在平面直角坐標系中,∠DCB=30°,AB邊在y軸上,點D的橫坐標為6,CQ⊥x軸,垂足為Q,點Q的橫坐標為12,過CD的直線l交x軸于點E,E點坐標為(18,0).
已知直角梯形ABCD如圖放置在平面直角坐標系中,∠DCB=30°,AB邊在y軸上,點D的橫坐標為6,CQ⊥x軸,垂足為Q,點Q的橫坐標為12,過CD的直線l交x軸于點E,E點坐標為(18,0).查看答案和解析>>
科目:初中數學 來源: 題型:
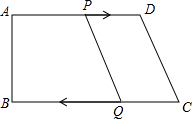 C同時出發,當其中一點到達端點時,另一點也隨之停止運動,設運動時間為t.
C同時出發,當其中一點到達端點時,另一點也隨之停止運動,設運動時間為t.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com