
【題目】如圖,已知拋物線![]() 經過點
經過點![]() 、
、![]() 和
和![]() ,
,![]() 垂直于
垂直于![]() 軸,交拋物線于點
軸,交拋物線于點![]() ,
,![]() 垂直于
垂直于![]() 軸,垂足為
軸,垂足為![]() ,直線
,直線![]() 是該拋物線的對稱軸,點
是該拋物線的對稱軸,點![]() 是拋物線的頂點.
是拋物線的頂點.

(1)求出該二次函數的表達式及點![]() 的坐標;
的坐標;
(2)若![]() 沿
沿![]() 軸向右平移,使其直角邊
軸向右平移,使其直角邊![]() 與對稱軸
與對稱軸![]() 重合,再沿對稱軸
重合,再沿對稱軸![]() 向上平移到點
向上平移到點![]() 與點
與點![]() 重合,得到
重合,得到![]() ,求此時
,求此時![]() 與矩形
與矩形![]() 重疊部分圖形的面積;
重疊部分圖形的面積;
(3)若![]() 沿
沿![]() 軸向右平移
軸向右平移![]() 個單位長度(
個單位長度(![]() )得到
)得到![]() ,
,![]() 與
與![]() 重疊部分圖形的面積記為
重疊部分圖形的面積記為![]() ,求
,求![]() 與
與![]() 之間的函數表達式,并寫出自變量
之間的函數表達式,并寫出自變量![]() 的取值范圍.
的取值范圍.
【答案】(1)拋物線的解析式為![]() ,點
,點![]() 的坐標為
的坐標為![]() ;(2)
;(2) ![]() ; (3)
; (3) 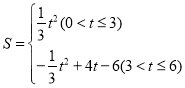 .
.
【解析】
(1)將點A(-3,0)、B(9,0)和C(0,4)代入y=ax2+bx+c即可求出該二次函數表達式,因為CD垂直于y軸,所以令y=4,求出x的值,即可寫出點D坐標;
(2)設A1F交CD于點G,O1F交CD于點H,求出頂點坐標,證△FGH∽△FA1O1,求出GH的長,因為Rt△A1O1F與矩形OCDE重疊部分的圖形是梯形A1O1HG,所以S重疊部分=![]() -S△FGH,即可求出結果;
-S△FGH,即可求出結果;
(3)當0<t≤3時,設O2C2交OD于點M,證△OO2M∽△OED,求出O2M=![]() t,可直接求出S=
t,可直接求出S=![]() =
=![]() OO2×O2M=
OO2×O2M=![]() t2;當3<t≤6時,設A2C2交OD于點M,O2C2交OD于點N,分別求出直線OD與直線A2C2的解析式,再求出其交點M的坐標,證△DC2N∽△DCO,求出C2N=
t2;當3<t≤6時,設A2C2交OD于點M,O2C2交OD于點N,分別求出直線OD與直線A2C2的解析式,再求出其交點M的坐標,證△DC2N∽△DCO,求出C2N=![]() (6-t),由S=S四邊形A2Q2NM=
(6-t),由S=S四邊形A2Q2NM=![]() ,可求出S與t的函數表達式.
,可求出S與t的函數表達式.
(1)∵拋拋線![]() 經過點
經過點![]() 、
、![]() 和
和![]() ,
,
∴拋物線的解析式為![]() ,
,
∵點![]() 在拋物線上,
在拋物線上,
∴![]() ,
,
∴![]() ,
,
∴拋物線的解析式為:![]() ,
,
∵![]() 垂直于
垂直于![]() 軸,
軸,![]() ,
,
令![]() ,
,
解得,![]() 或
或![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ;
;
(2)如圖1所示,設![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,
∵點![]() 是拋物線
是拋物線![]() 的頂點,
的頂點,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴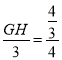 ,
,
解得,![]() ,
,
∵![]() 與矩形
與矩形![]() 重疊部分的圖形是梯形
重疊部分的圖形是梯形![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
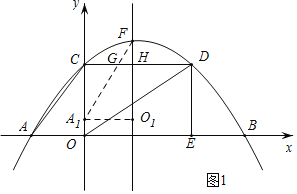
(3)①當![]() 時,如圖2所示,設
時,如圖2所示,設![]() 交
交![]() 于點
于點![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
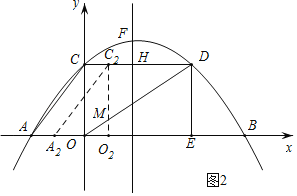
②當![]() 時,如圖3所示,設
時,如圖3所示,設![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,
將點![]() 代入
代入![]() ,
,
得,![]() ,
,
∴![]() ,
,
將點![]() ,
,![]() 代入
代入![]() ,
,
得,![]() ,
,
解得,![]() ,
,![]() ,
,
∴直線![]() 的解析式為:
的解析式為:![]() ,
,
聯立![]() 與
與![]() ,
,
得,![]() ,
,
解得,![]() ,
,
∴兩直線交點![]() 坐標為
坐標為![]() ,
,
故點![]() 到
到![]() 2的距離為
2的距離為![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
∴![]() 與
與![]() 的函數關系式為:
的函數關系式為: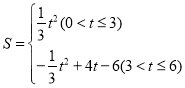 .
.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 、點
、點![]() 分別在線段
分別在線段![]() 、線段
、線段![]() 上運動(不包含端點),以
上運動(不包含端點),以![]() 為邊作平行四邊形
為邊作平行四邊形![]() ,點
,點![]() 從
從![]() 向
向![]() 運動,速度為每秒
運動,速度為每秒![]() 個單位長度,點
個單位長度,點![]() 從
從![]() 向
向![]() 運動,速度為每秒
運動,速度為每秒![]() 個單位長度,兩點同時出發,當一個點到達終點時,兩點都停止運動,運動時間為
個單位長度,兩點同時出發,當一個點到達終點時,兩點都停止運動,運動時間為![]() 秒.
秒.
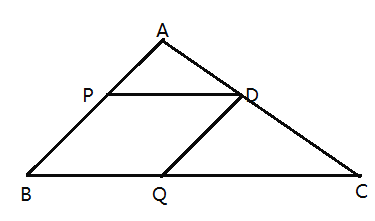
(1)![]() __ ,
__ ,![]() __ _; (用
__ _; (用![]() 表示)
表示)
(2)當平行四邊形![]() 為菱形時,求出
為菱形時,求出![]() 值;
值;
(3)![]() 點能否落在線段
點能否落在線段![]() 上?若能,求出
上?若能,求出![]()
(4)當![]() 分別與線段
分別與線段![]() 交于
交于![]() 兩點時,求
兩點時,求![]() 長度的范圍;
長度的范圍;
(5)平行四邊形![]() 的面積能否為
的面積能否為![]() 面積的一半,若能,請求出
面積的一半,若能,請求出![]() 值,若不能,請說明理由.
值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
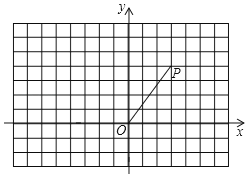
【題目】如圖,在平面直角坐標系中,點P(3,4),連接OP,將線段OP繞點O逆時針旋轉90°得線段OP1.
(1)在圖中作出線段OP1,并寫出P1點的坐標;
(2)求點P在旋轉過程中所繞過的路徑長;
(3)求線段OP在旋轉過程中所掃過的圖形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年5月5日,中國郵政發行《馬克思誕辰200周年》紀念郵票1套2枚(如圖),這套郵票正面圖案為:馬克思像、馬克思與恩格斯像,背面完全相同.發行當日,小宇購買了此款紀念郵票2套,他將2套郵票沿中間虛線撕開(使4枚形狀、大小完全相同)后將4枚紀念郵票背面朝上放在桌面上,并隨機從中抽出2張,則抽出的2張郵票恰好都是“馬克思像”的概率為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一汽車租賃公司擁有某種型號的汽車100輛.公司在經營中發現每輛車的月租金x(元)與每月租出的車輛數(y)有如下關系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)觀察表格,用所學過的一次函數、反比例函數或二次函數的有關知識求出每月租出的車輛數y(輛)與每輛車的月租金x(元)之間的關系式.
(2)已知租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.用含x(x≥3000)的代數式填表:
租出的車輛數 | 未租出的車輛數 | ||
租出每輛車的月收益 | 所有未租出的車輛每月的維護費 |
(3)若你是該公司的經理,你會將每輛車的月租金定為多少元,才能使公司獲得最大月收益?請求出公司的最大月收益是多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市用1200元購進一批甲玩具,用800元購進一批乙玩具,所購甲玩具件數是乙玩具件數的![]() ,已知甲玩具的進貨單價比乙玩具的進貨單價多1元.
,已知甲玩具的進貨單價比乙玩具的進貨單價多1元.
(1)求:甲、乙玩具的進貨單價各是多少元?
(2)玩具售完后,超市決定再次購進甲、乙玩具(甲、乙玩具的進貨單價不變),購進乙玩具的件數比甲玩具件數的2倍多60件,求:該超市用不超過2100元最多可以采購甲玩具多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,且AB=12,點C為半圓上的一點.將此半圓沿BC所在的直線折疊,若圓弧BC恰好過圓心O,則圖中陰影部分的面積是( )

A. 4πB. 5πC. 6πD. 8π
查看答案和解析>>
科目:初中數學 來源: 題型:
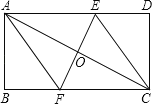
【題目】已知如圖,矩形ABCD的周長為64,AB=12,對角線AC的垂直平分線分別交AD、BC于E、F,連接AF、CE、EF,且EF與AC相交于點O.
(1)求證:四邊形AECF是菱形;
(2)求S△ABF與S△AEF的比值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com