【題目】某公司共有A、B、C三個部門，根據每個部門的員工人數和相應每人所創的年利潤繪制成如下的統計表和扇形圖
（1）①在扇形圖中，C部門所對應的圓心角的度數為
②在統計表中，b= ，c=
（2）求這個公司平均每人所創年利潤．
【答案】（1）①108°；②b=9,c=6；（2）7.6萬元
【解析】試題分析：（1）①根據扇形圓心角的度數=部分占總體的百分比×360°進行計算即可；②先求得A部門的員工人數所占的百分比，進而得到各部門的員工總人數，據此可得B，C部門的人數；
（2）根據總利潤除以總人數，即可得到這個公司平均每人所創年利潤．
試題解析：
（1）①在扇形圖中，C部門所對應的圓心角的度數為：360°×30%=108°；
②A部門的員工人數所占的百分比為：1﹣30%﹣45%=25%，
各部門的員工總人數為：5÷25%=20（人），
∴b=20×45%=9，c=20×30%=6，
故答案為：108°，9，6；
（2）這個公司平均每人所創年利潤為: 
（萬元）．
開心蛙狀元測試卷系列答案科目：初中數學 來源： 題型：
【題目】閱讀以下兩則材料，解決后續問題：
材料一：我們可以將任意三位數記為
(其中a,b,c,分別表示該數的百位數字、十位數字和個位數字，且a≠0，顯然=100a+10b+c.
材料二：若一個三位數的三個數字均不為0且三個數字互不相等，則稱之為原始數，比如123就是一個原始數.將原始數的三個數位數字交換順序，可產生出5個新的原始數，比如由123可以產生出132、213、231、312、321這5個新原始數.將這6個數相加，得到的和1332稱為由原始數123生成的終止數.
問題：（1）求原始數247生成的終止數；
（2）試說明所有的原始數生成的終止數都能被222整除；
（3）若一個原始數生成的終止數為
，求滿足條件的所有原始數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是菱形，對角線AC、BD相交于點O，DH⊥AB于H，連接OH，
（1）求證：∠DHO=∠DCO．
（2）若OC=4，BD=6，求菱形ABCD的周長和面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
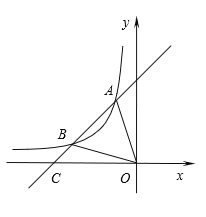
【題目】如圖，一次函數y＝x+4的圖像與反比例函數
（k為常數且k≠0）的圖像交于A（－1，a），B（b，1）兩點，與x軸交于點C．
（1）求此反比例函數的表達式；
（2）若點P在x軸上，且
，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩人各射擊
次，甲所中的環數是
，
，，
，
，
，且甲所中的環數的平均數是，眾數是；乙所中的環數的平均數是，方差是4.根據以上數據，對甲，乙射擊成績的正確判斷是（ ）
A.甲射擊成績比乙穩定B.乙射擊成績比甲穩定
C.甲，乙射擊成績穩定性相同D.甲、乙射擊成績穩定性無法比較
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】同學們都知道
表示5與(-2)之差的絕對值,也可理解為5與-2兩數在數軸上所對的兩點之間的距離,試探索:
(1) 求= ;
(2) 使得
=3成立的數是 ;
(3) 由以上探索猜想,對于任何有理數x,則
最小值是 ;
(4)由以上探索猜想,使得
的成立的整數x是
查看答案和解析>>
科目：初中數學 來源： 題型：
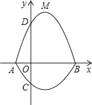
【題目】如圖，在平面直角坐標系xOy中，A、B為x軸上兩點，C、D為y軸上的兩點，經過點A、C、B的拋物線的一部分c1與經過點A、D、B的拋物線的一部分c2組合成一條封閉曲線，我們把這條封閉曲線成為“蛋線”．已知點C的坐標為（0，﹣
），點M是拋物線C2：y=mx2﹣2mx﹣3m（m＜0）的頂點．
（1）求A、B兩點的坐標；
（2）“蛋線”在第四象限上是否存在一點P，使得△PBC的面積最大？若存在，求出△PBC面積的最大值；若不存在，請說明理由；
（3）當△BDM為直角三角形時，求m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】國慶節放假時，小華一家三口一起乘小轎車去鄉下探望爺爺、奶奶和外公、外婆．早上從家里出發，向東走了4千米到超市買東西，然后又向東走了3千米到爺爺家，中午從爺爺家出發向西走了12千米到外公家，晚上返回家里．
（1）若以家為原點，向東為正方向，用1個單位長度表示1千米，請將超市、爺爺家和外公家的位置在下面數軸上分別用點A、B、C表示出來；
（2）若小轎車每千米耗油0.09升，求小明一家從出發到返回家所經歷路程小車的耗油量．（精確到0.1升）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，
，點
在線段
上運動（不與
、
重合），連接
，作
，
交線段
于
.
（1）當
時，
= ，
= ；點從向運動時，
逐漸 （填“增大”或“減小”）；
（2）當
等于多少時，
，請說明理由；
（3）在點的運動過程中，
的形狀可以是等腰三角形嗎？若可以，請直接寫出的度數.若不可以，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com