
【題目】已知:O是直線AB上一點,∠COD是直角,OE平分∠BOC

(1)如圖1,若∠AOC=30°,求∠DOE的度數。
(2)如圖1,若∠AOC=![]() ,直接寫出∠DOE的度數。(用含的代數式表示)
,直接寫出∠DOE的度數。(用含的代數式表示)
(3)將圖1中的∠DOC繞頂點O順時針旋轉至圖2的位置,其它條件不變,探究∠AOC和∠DOE的度數之間的關系,寫出結論,并說明理由。
(4)在圖2中,若∠AOC內部有一條射線OF,且滿足∠AOC-4∠AOF=2∠BOE,其它條件不變,試寫出∠AOF與∠DOE度數的關系(不寫過程)
【答案】(1)15°;(2)∠DOE=![]()
![]() ;(3)證明見解析;(4)∠DOE=∠AOF+45°.
;(3)證明見解析;(4)∠DOE=∠AOF+45°.
【解析】
(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度數;
(2)由(1)可得出結論∠DOE=![]() ∠AOC,從而用含a的代數式表示出∠DOE的度數;
∠AOC,從而用含a的代數式表示出∠DOE的度數;
(3)由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,則得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),從而得出∠AOC和∠DOE的度數之間的關系;
(4)設∠DOE=x,∠AOF=y,根據已知和:∠AOC-4∠AOF=2∠BOE,結合圖形可得出∠DOE=∠AOF+45°.
解:(1)∵∠AOC=30∴∠COB=150,
又 ∵OE平分∠BOC, ∴∠COE=75,
而∠COD=90,∴∠DOE=15 ;
(2)∠DOE=![]()
![]() ;
;
(3)設∠AOC=![]() ,則∠BOC=180-
,則∠BOC=180-![]() ,
,
又∵OE平分∠BOC, ∴∠COE=![]() (180°-
(180°-![]() =90°-
=90°-![]()
![]() .
.
又∵∠DOE=90,
∴∠DOE=90-(90-![]()
![]() )=-
)=-![]()
![]() ,
,
∴∠DOE=-![]() ∠AOC ;
∠AOC ;
(4)∠DOE=∠AOF+45°.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案科目:初中數學 來源: 題型:
【題目】如圖是某班全體學生外出時選擇乘車、步行、騎車人數的條形統計圖和扇形統計圖(兩圖都不完整),則下列結論中正確的是( )

A. 步行人數為30人 B. 騎車人數占總人數的10%
C. 該班總人數為50人 D. 乘車人數是騎車人數的40%
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習了“求簡單隨機事件發生的可能性大小”知識后,小敏,小聰,小麗三人分別編寫了一道有關隨機事件的試題并進行了解答.小敏,小聰,小麗編寫的試題分別是下面的(1)(2)(3).
(1)一個不透明的盒子里裝有4個紅球,2個白球,除顏色外其它都相同,攪均后,從中隨意摸出一個球,摸出紅球的可能性是多少?解:P(摸出一個紅球)=![]() .
.
(2)口袋里裝有如圖所示的1角硬幣2枚、5角硬幣2枚、1 元硬幣1枚.攪均后,從中隨意摸出一枚硬幣,摸出1角硬幣的可能性是多少?解:P(摸出1角的硬幣)=![]() .
.
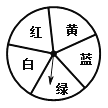
(3)如圖,是一個轉盤,盤面上有5個全等的扇形區域,每個區域顯示有不同的顏色,輕輕轉動轉盤,當轉盤停止后,指針對準紅色區域的可能性是多少?解:P(指針對準紅色區域)=![]() .
.
問題:根據以上材料回答問題:小敏,小聰,小麗三人中,誰編寫的試題及解答是正確的,并簡要說明其他兩人所編試題或解答的不足之處.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,扇形AOD中,∠AOD=90°,OA=6,點P為![]() 上任意一點(不與點A和D重合),
上任意一點(不與點A和D重合),
PQ⊥OD于點Q,點I為△OPQ的內心,過O、I和D三點的圓的半徑為r,則當點P在![]() 上運動時,求r的值.
上運動時,求r的值.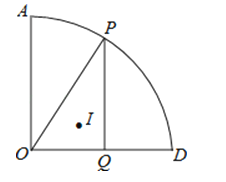
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一項工程,甲乙兩人合作需要8天完成任務,若甲單獨做需要12天完成任務.
(1)若甲乙兩人一起做6天,剩下的由甲單獨做,還需要幾天完成?
(2)若甲乙兩人一起做4天,剩下的由乙單獨做,還需要幾天完成?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角梯形ABCD中,以AD為直徑的半圓與BC相切于E,BO交半圓于F,DF的延長線交AB于點P,連DE.以下結論:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4ABDC.其中正確的是( )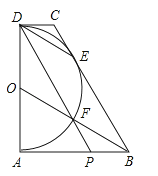
A.①②③④
B.只有①②
C.只有①②④
D.只有③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的內切圓,點D、E分別為邊AC、BC上的點,且DE為⊙O的切線,若△ABC的周長為25,BC的長是9,則△ADE的周長是( )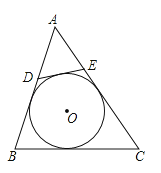
A.7
B.8
C.9
D.16
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課本中有一探究活動:如圖1,有甲、乙兩個三角形,甲三角形內角分別為10°,20°,150°;乙三角形內角分別為80°,25°,75°.你能把每一個三角形分成兩個等腰三角形嗎?畫一畫,并標出每個等腰三角形頂角的度數.
(1)小明按要求畫出了圖1中甲圖的分割線,請你幫他作出圖1中乙圖的分割線;
(2)小明進一步探究發現:能將一個頂角為108°的等腰三角形分成三個等腰三角形;請在圖2中用兩種不同的方法畫出分割線,并標注每個等腰三角形頂角的度數;(若兩種方法分得的三角形成3對全等三角形,則視為同一種方法)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:正整數n的“H運算”是:①當n為奇數時,H=3n+13;②當n為偶數時,H=n![]() …(連續乘以
…(連續乘以![]() ,一直算到H為奇數止).如:數3經過“H運算”的結果是22,經過2次“H運算”的結果為11,經過三次“H運算”的結果為46,那么257經2017次“H運算”得到的結果是( )
,一直算到H為奇數止).如:數3經過“H運算”的結果是22,經過2次“H運算”的結果為11,經過三次“H運算”的結果為46,那么257經2017次“H運算”得到的結果是( )
A. 161 B. 1 C. 16 D. 以上答案均不正確
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com