
【題目】為保護美麗如畫的邛海濕地,西昌市污水處理廠決定先購買![]() 兩型污水處理設備共20臺,對濕地周邊污水進行處理.每臺
兩型污水處理設備共20臺,對濕地周邊污水進行處理.每臺![]() 型污水處理設備12萬,每臺
型污水處理設備12萬,每臺![]() 型污水處理設備10萬,已知2臺
型污水處理設備10萬,已知2臺![]() 型污水處理設備和1臺
型污水處理設備和1臺![]() 型污水處理設備每周處理污水680噸,3臺
型污水處理設備每周處理污水680噸,3臺![]() 型污水處理設備和2臺
型污水處理設備和2臺![]() 型污水處理設備每周處理污水1120噸.
型污水處理設備每周處理污水1120噸.
(1)求每臺![]() 、
、![]() 型污水處理設備每周分別可以處理污水多少噸?
型污水處理設備每周分別可以處理污水多少噸?
(2)經預算,污水處理廠購買設備的資金不超過230萬元,每周處理污水的量不低于4500噸,請列舉出所有購買方案,并指出所需購買資金最少的方案及最少資金.
【答案】(1)![]() 型污水處理設備每周每臺可以處理污水240噸,
型污水處理設備每周每臺可以處理污水240噸,![]() 型污水處理設備每周每臺可以處理污水200噸;(2)第一種方案:即購買
型污水處理設備每周每臺可以處理污水200噸;(2)第一種方案:即購買![]() 型污水處理設備13臺,購買
型污水處理設備13臺,購買![]() 型污水處理設備7臺;第二種方案:即購買
型污水處理設備7臺;第二種方案:即購買![]() 型污水處理設備14臺,購買
型污水處理設備14臺,購買![]() 型污水處理設備6臺;第三種方案;即購買
型污水處理設備6臺;第三種方案;即購買![]() 型污水處理設備15臺,購買
型污水處理設備15臺,購買![]() 型污水處理設備5臺;應該選擇第一種方案,資金最少是226萬元
型污水處理設備5臺;應該選擇第一種方案,資金最少是226萬元
【解析】
(1)設![]() 型污水處理設備每周每臺可以處理污水
型污水處理設備每周每臺可以處理污水![]() 噸,
噸,![]() 型污水處理設備每周每臺可以處理污水
型污水處理設備每周每臺可以處理污水![]() 噸,根據題意得到二元一次方程組即可求解;
噸,根據題意得到二元一次方程組即可求解;
(2)設購買![]() 型污水處理設備
型污水處理設備![]() 臺,則購買
臺,則購買![]() 型污水處理設備
型污水處理設備![]() 臺,根據題意得到不等式組,即可得到3種方案,分別求出各方案的費用即可比較求解.
臺,根據題意得到不等式組,即可得到3種方案,分別求出各方案的費用即可比較求解.
解:(1)設![]() 型污水處理設備每周每臺可以處理污水
型污水處理設備每周每臺可以處理污水![]() 噸,
噸,![]() 型污水處理設備每周每臺可以處理污水
型污水處理設備每周每臺可以處理污水![]() 噸,
噸,
![]()
解得![]()
即![]() 型污水處理設備每周每臺可以處理污水240噸,
型污水處理設備每周每臺可以處理污水240噸,![]() 型污水處理設備每周每臺可以處理污水200噸;
型污水處理設備每周每臺可以處理污水200噸;
(2)設購買![]() 型污水處理設備
型污水處理設備![]() 臺,則購買
臺,則購買![]() 型污水處理設備
型污水處理設備![]() 臺,
臺,
則![]()
解得,![]() ,
,
∵![]() 為正整數,
為正整數,![]() 或14或15
或14或15
第一種方案:即購買![]() 型污水處理設備13臺,購買
型污水處理設備13臺,購買![]() 型污水處理設備7臺;
型污水處理設備7臺;
第二種方案:即購買![]() 型污水處理設備14臺,購買
型污水處理設備14臺,購買![]() 型污水處理設備6臺;
型污水處理設備6臺;
第三種方案;即購買![]() 型污水處理設備15臺,購買
型污水處理設備15臺,購買![]() 型污水處理設備5臺;
型污水處理設備5臺;
∵第一種方案所需資金:![]() 萬元;
萬元;
第二種方案所需資金:![]() 萬元;
萬元;
第三種方案所需資金:![]() 萬元;
萬元;
從節約資金的角度考慮,應該選擇第一種方案,即購買![]() 型污水處理設備13臺,購買
型污水處理設備13臺,購買![]() 型污水處理設備7臺;
型污水處理設備7臺;
∴選擇第一種方案所需資金最少,最少是226萬元.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案科目:初中數學 來源: 題型:
【題目】小華將一條直角邊長為1的一個等腰直角三角形紙片(如圖1),沿它的對稱軸折疊1次后得到一個等腰直角三角形(如圖2),再將圖2的等腰直角三角形沿它的對稱軸折疊后得到一個等腰直角三角形(如圖3),則圖3中的等腰直角三角形的一條腰長為;同上操作,若小華連續將圖1的等腰直角三角形折疊n次后所得到的等腰直角三角形(如圖n+1)的一條腰長為 . 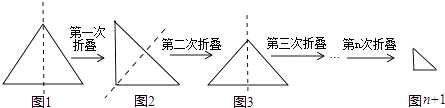
查看答案和解析>>
科目:初中數學 來源: 題型:
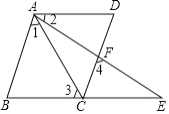
【題目】填空:已知:如圖,![]() 、
、![]() 、
、![]() 三點在同一直線上,
三點在同一直線上,![]() 、
、![]() 、
、![]() 三點在同一直線上,
三點在同一直線上,![]() ,
,![]() .求證:
.求證:![]() .
.
證明:∵![]()
∴________(內錯角相等,兩直線平行)
∴![]() ________(兩直線平行,內錯角相等)
________(兩直線平行,內錯角相等)
∵![]()
∴![]() (________________)
(________________)
∵![]()
∴![]() ,(________________)
,(________________)
即![]() ________
________
∴![]()
∴![]() (同位角相等,兩直線平行).
(同位角相等,兩直線平行).
查看答案和解析>>
科目:初中數學 來源: 題型:
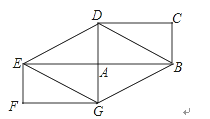
【題目】如圖,矩形ABCD和矩形AEFG關于點A中心對稱,
(1)四邊形BDEG是菱形嗎?請說明理由.
(2)若矩形ABCD面積為8,求四邊形BDEG的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰![]() 中,
中,![]() ,點
,點![]() 是直線
是直線![]() 上一點(不與
上一點(不與![]() 重合),以
重合),以![]() 為一邊在
為一邊在![]() 的右側作等腰
的右側作等腰![]() ,使
,使![]() ,
,![]() ,連結
,連結![]() .
.
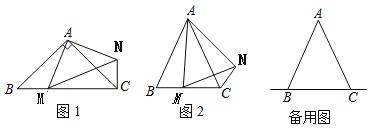
(1)如圖1,當點![]() 在線段
在線段![]() 上時,如果
上時,如果![]() ,則
,則![]() _______°.
_______°.
(2)設![]() .
.
①如圖2,當點![]() 在線段
在線段![]() 上移動時,
上移動時,![]() 之間有怎樣的數量關系?請說明理由.
之間有怎樣的數量關系?請說明理由.
②當點![]() 在直線
在直線![]() 上移動時,
上移動時,![]() 之間有怎樣的數量關系?請你直接寫出你的結論.
之間有怎樣的數量關系?請你直接寫出你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的對角線AC、BD交于點O,AE平分∠BAD交BC于點E,且∠ADC=60°,AB=![]() BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的個數有( )
BC,成立的個數有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點D,E分別是邊BC,AB上的中點,連接DE并延長至點F,使EF=2DE,連接CE、AF.
(1)證明:AF=CE;
(2)當∠B=30°時,試判斷四邊形ACEF的形狀并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC為等腰直角三角形,∠ACB=90°,拋物線y=﹣x2+bx+c經過A,B兩點,其中點A,C的坐標分別為(1,0),(﹣4,0),拋物線的頂點為點D.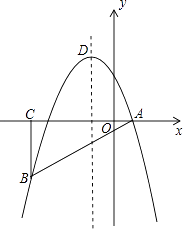
(1)求拋物線的解析式;
(2)點E是直角三角形ABC斜邊AB上的一個動點(不與A,B重合),過點E作x軸的垂線,交拋物線于點F,當線段FE的長度最大時,求點E的坐標;
(3)在(2)的條件下,拋物線上是否存在一點P,使△PEF是以EF為直角邊的直角三角形?若存在,求出所有點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com