Question

如圖，Rt△ABC中，∠C=90°，BC=6，AC=8．點P，Q都是斜邊AB上的動點，點P從B 向A運動（不與點B重合），點Q從A向B運動，BP=AQ．點D，E分別是點A，B以Q，P為對稱中心的對稱點， HQ⊥AB于Q，交AC于點H．當點E到達頂點A時，P，Q同時停止運動．設BP的長為x，△HDE的面積為y．

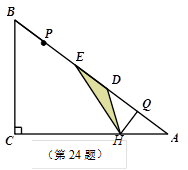
（1）求證：△DHQ∽△ABC；

（2）求y關于x的函數解析式并求y的最大值；

（3）當x為何值時，△HDE為等腰三角形？

 

Answer 1

 

（1）略

（2）

（3）當x的值為時，△HDE是等腰三角形

解析:（14分）

（1）∵A、D關于點Q成中心對稱，HQ⊥AB，

∴=90°，HD=HA，

∴，…………………………………………………………………………3分

∴△DHQ∽△ABC． ……………………………………………………………………1分

 

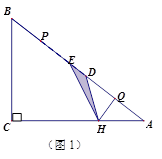
（2）①如圖1，當時，

ED=，QH=，

此時． …………………………………………3分

當時，最大值．

②如圖2，當時，

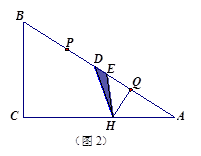
ED=，QH=，

此時． …………………………………………2分

當時，最大值．

∴y與x之間的函數解析式為

y的最大值是．……………………………………………………………………1分

（3）①如圖1，當時，

若DE=DH，∵DH=AH=， DE=，

∴=，．

顯然ED=EH，HD=HE不可能； ……………………………………………………1分

②如圖2，當時，

若DE=DH，=，；   …………………………………………1分

若HD=HE，此時點D，E分別與點B，A重合，；  ………………………1分

若ED=EH，則△EDH∽△HDA，

∴，，．   ……………………………………1分

∴當x的值為時，△HDE是等腰三角形.

（其他解法相應給分）