
【題目】根據下列要求,解答相關問題.
請補全以下求不等式﹣2x2﹣4x>0的解集的過程.
①構造函數,畫出圖象:根據不等式特征構造二次函數y=﹣2x2﹣4x;并在下面的坐標系中(圖1)畫出二次函數y=﹣2x2﹣4x的圖象(只畫出圖象即可).
②求得界點,標示所需,當y=0時,求得方程﹣2x2﹣4x=0的解為多少?;并用鋸齒線標示出函數y=﹣2x2﹣4x圖象中y>0的部分.
③借助圖象,寫出解集:由所標示圖象,可得不等式﹣2x2﹣4x>0的解集為﹣2<x<0.請你利用上面求一元一次不等式解集的過程,求不等式x2﹣2x+1≥4的解集.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=mx+n(m≠0)的圖象與反比例函數y=![]() (k≠0)的圖象交于第一、三象限內的A、B兩點,與y軸交于點C,過點B作BM⊥x軸,垂足為M,BM=OM,OB=2
(k≠0)的圖象交于第一、三象限內的A、B兩點,與y軸交于點C,過點B作BM⊥x軸,垂足為M,BM=OM,OB=2![]() ,點A的縱坐標為4.
,點A的縱坐標為4.
(1)求該反比例函數和一次函數的解析式;
(2)連接MC,求四邊形MBOC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】頤和園是我國現存規模最大,保存最完整的古代皇家園林,它和承德避暑山莊、蘇州拙政園、蘇州留園并稱為中國四大名園.該園有一個六角亭,如果它的地基是半徑為2米的正六邊形,那么這個地基的面積是米2 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋中裝有5個黃球、13個黑球和22個紅球,它們除顏色外都相同。
(1)求從袋中摸出一個球是黃球的概率;
(2)現從袋中取出若干個黑球,并放入相同數量的黃球,攪拌均勻后,使從袋中摸出一個球是黃球的概率不小于![]() ,問至少取出了多少個黑球?
,問至少取出了多少個黑球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖的2016年6月份的日歷表中,任意框出表中豎列上三個相鄰的數,這三個數的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,點O是等邊△ABC內的任一點,連接OA,OB,OC.
(1)如圖1,已知∠AOB=150°,∠BOC=120°,將△BOC繞點C按順時針方向旋轉60°得△ADC.
①∠DAO的度數是多少?
②用等式表示線段OA,OB,OC之間的數量關系,并證明;
(2)設∠AOB=α,∠BOC=β.
①當α,β滿足什么關系時,OA+OB+OC有最小值?請在圖2中畫出符合條件的圖形,并說明理由;
②若等邊△ABC的邊長為1,直接寫出OA+OB+OC的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=2(x+1)(x﹣a),其中a>0,若當x≤2時,y隨著x增大而減小,當x≥2時y隨著x的增大而增大,則a的值是( )
A.3
B.5
C.7
D.不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在扇形OAB中,∠AOB=90°,OA=3,將扇形OAB繞點A逆時針旋轉n°(0<n<180)后得到扇形O′AB′,當點O在弧AB′上時,n為 , 圖中陰影部分的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,點E是BC邊上一點,∠DEF=45°且角的兩邊分別與邊AB,射線CA交于點P,Q.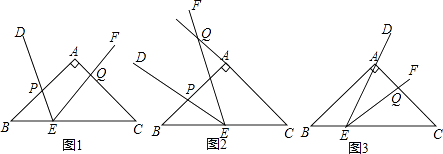
(1)如圖2,若點E為BC中點,將∠DEF繞著點E逆時針旋轉,DE與邊AB交于點P,EF與CA的延長線交于點Q.設BP為x,CQ為y,試求y與x的函數關系式,并寫出自變量x的取值范圍;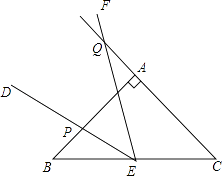
(2)如圖3,點E在邊BC上沿B到C的方向運動(不與B,C重合),且DE始終經過點A,EF與邊AC交于Q點.探究:在∠DEF運動過程中,△AEQ能否構成等腰三角形,若能,求出BE的長;若不能,請說明理由.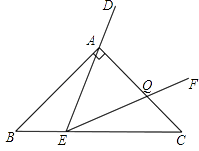
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com