
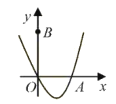
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點.拋物線
為坐標原點.拋物線![]() 與
與![]() 軸正半軸交于點
軸正半軸交于點![]() ,點
,點![]() 的坐標為
的坐標為![]() ,
,![]() 是該拋物線第一象限圖像上的一點,
是該拋物線第一象限圖像上的一點,![]() 三點均在某一個正方形的邊上,且該正方形的任何一條邊均與某條坐標軸平行,設點
三點均在某一個正方形的邊上,且該正方形的任何一條邊均與某條坐標軸平行,設點![]() 的橫坐標為
的橫坐標為![]() .若這個正方形的面積最小,則
.若這個正方形的面積最小,則![]() 的取值范圍是__________.
的取值范圍是__________.
【答案】![]()
【解析】
根據拋物線![]() 與x軸正半軸交于點A,得點A坐標為(2,0),點B的坐標為(0,3),可得最小正方形的邊長為3,最小正方形的面積為9,根據題意可得A、B、C中任意兩個點不能重合,故此可以確定點C的橫坐標的取值范圍.
與x軸正半軸交于點A,得點A坐標為(2,0),點B的坐標為(0,3),可得最小正方形的邊長為3,最小正方形的面積為9,根據題意可得A、B、C中任意兩個點不能重合,故此可以確定點C的橫坐標的取值范圍.
解:∵拋物線![]() 與x軸正半軸交于點A,
與x軸正半軸交于點A,
∴點A的坐標為(2,0),
如圖所示:
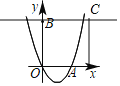
當A,B,C三點均在某一個正方形的邊上, 且該正方形的任何一條邊均與某條坐標軸平行,
∵點B的坐標為(0,3), 正方形的面積最小時, 此時正方形的邊長為3,
∴過點A、B、C的正方形的面積最小值為9,
∴S≥9.
當y=3時,![]() 解得
解得![]()
∴當2<m≤3,時, 正方形面積有最小值;
當m=-1時, 正方形最小邊長也為3, 正方形面積也有最小值,
∵C在第一象限,m>0,
綜上所述:點C的橫坐標m的取值范圍是: 2<m≤3.
故答案為:2<m≤3.


科目:初中數學 來源: 題型:
【題目】《小豬佩奇》這部動畫片,估計同學們都非常喜歡.周末,小豬佩奇一家4口人(小豬佩奇,小豬喬治,小豬媽媽,小豬爸爸)到一家餐廳就餐,包廂有一圓桌,旁邊有四個座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小豬佩奇隨機坐到![]() 座位的概率是________;
座位的概率是________;
(2)若現在由小豬佩奇,小豬喬治兩人先后選座位,用樹狀圖或列表的方法計算出小豬佩奇和小豬喬治坐對面的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
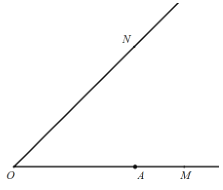
【題目】如圖,已知![]() ,
,![]() 為射線
為射線![]() 上一定點,點
上一定點,點![]() 關于射線
關于射線![]() 的對稱點為點
的對稱點為點![]() 為射線
為射線![]() 上一動點,連接
上一動點,連接![]() ,滿足
,滿足![]() 為鈍角,以點
為鈍角,以點![]() 為中心,將線段
為中心,將線段![]() 逆時針旋轉
逆時針旋轉![]() 至線段
至線段![]() ,滿足點
,滿足點![]() 在射線
在射線![]() 的反向延長線上.
的反向延長線上.
(1)依題意補全圖形;
(2)當點![]() 在運動過程中,旋轉角
在運動過程中,旋轉角![]() 是否發生變化?若不變化,請求出
是否發生變化?若不變化,請求出![]() 的值,若變化,請說明理由;
的值,若變化,請說明理由;
(3)從點![]() 向射線
向射線![]() 作垂線,與射線
作垂線,與射線![]() 的反向延長線交于點
的反向延長線交于點![]() ,探究線段
,探究線段![]() 和
和![]() 的數量關系并證明.
的數量關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為調查某市市民上班時最常用的交通工具的情況,隨機抽取了部分市民進行調查,要求被調查者從“![]() :自行車,
:自行車,![]() :家庭汽車,
:家庭汽車,![]() :公交車,
:公交車,![]() :電動車,
:電動車,![]() :其他”五個選項中選擇最常用的一項,將所有調查結果整理后繪制成如下不完整的條形統計圖和扇形統計圖,請結合統計圖回答下列問題.
:其他”五個選項中選擇最常用的一項,將所有調查結果整理后繪制成如下不完整的條形統計圖和扇形統計圖,請結合統計圖回答下列問題.
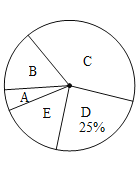
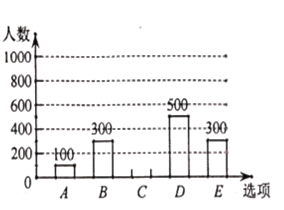
(1)本次調查中,一共調查了 名市民;扇形統計圖中,![]() 項對應的扇形圓心角是_____
項對應的扇形圓心角是_____ ![]() ;
;
(2)補全條形統計圖;
(3)若甲上班時從![]() 三種交通工具中隨機選擇一種, 乙上班時從
三種交通工具中隨機選擇一種, 乙上班時從![]() 三種交通工具中隨機選擇一種,請用列表法或畫樹狀圖的方法,求出甲、乙兩人都不選
三種交通工具中隨機選擇一種,請用列表法或畫樹狀圖的方法,求出甲、乙兩人都不選![]() 種交通工具上班的概率.
種交通工具上班的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是小安填寫的數學實踐活動報告的部分內容
題 目 | 測量鐵塔頂端到地面的高度 | |
測量目標示意圖 |
|
|
相關數據 | CD=20m,ɑ=45°,β=52° | |
求鐵塔的高度FE(結果精確到1米)(參考數據:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
查看答案和解析>>
科目:初中數學 來源: 題型:
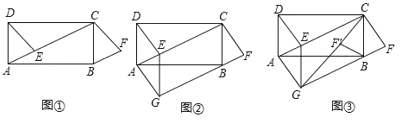
【題目】(操作)如圖①,在矩形![]() 中,
中,![]() 為對角線
為對角線![]() 上一點(不與點
上一點(不與點![]() 重合),將
重合),將![]() 沿射線
沿射線![]() 方向平移到
方向平移到![]() 的位置,
的位置,![]() 的對應點為
的對應點為![]() .已知
.已知![]() (不需要證明).
(不需要證明).
(探究)過圖①中的點![]() 作
作![]() 交
交![]() 延長線于點
延長線于點![]() ,連接
,連接![]() ,其它條件不變,如圖②.求證:
,其它條件不變,如圖②.求證:![]() .
.
(拓展)將圖②中的![]() 沿
沿![]() 翻折得到
翻折得到![]() ,連接
,連接![]() ,其它條件不變,如圖③.當
,其它條件不變,如圖③.當![]() 最短時,若
最短時,若![]() ,
,![]() ,直接寫出
,直接寫出![]() 的長和此時四邊形
的長和此時四邊形![]() 的周長.
的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩個工廠同時加工一批機器零件.甲工廠先加工了兩天后停止加工,維修設備,當維修完設備時,甲乙兩廠加工的零件數相等,甲工廠再以原來的工作效率繼續加工這批零件.甲乙兩廠加工零件的數量![]() (件),
(件),![]() (件)與加工件的時間
(件)與加工件的時間![]() (天)的函數圖象如圖所示,
(天)的函數圖象如圖所示,

(1)乙工廠每天加工零件的數為_____件;
(2)甲工廠維修設備的時間是多少天?
(3)求甲維修設備后加工零件的數量![]() (件)與加工零件的時間
(件)與加工零件的時間![]() (天)的函數關系式,并寫出自變量
(天)的函數關系式,并寫出自變量![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著新冠肺炎的爆發,市場對口罩的需求量急劇增大.某口罩生產商自二月份以來,--直積極恢復產能,每日口罩生產量![]() (百萬個)與天數
(百萬個)與天數![]() 且
且![]() 為整數)的函數關系圖象如圖所示,而該生產商對口供應市場對口罩的需求量<(百萬個)與天數
為整數)的函數關系圖象如圖所示,而該生產商對口供應市場對口罩的需求量<(百萬個)與天數![]() 呈拋物線型,第
呈拋物線型,第![]() 天市場口罩缺口(需求量與供應量差)就達到
天市場口罩缺口(需求量與供應量差)就達到![]() (百萬個),之后若干天,市場口罩需求量不斷上升,在第
(百萬個),之后若干天,市場口罩需求量不斷上升,在第![]() 天需求量達到最高峰
天需求量達到最高峰![]() (百萬個).
(百萬個).
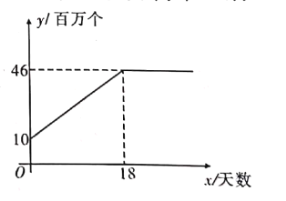
![]() 求出
求出![]() 與
與![]() 的函數解析式;
的函數解析式;
![]() 當市場供應量不小于需求量時,市民買口罩才無需提前預約,那么在整個二月份,市民無需預約即可購買口罩的天數共有多少天?
當市場供應量不小于需求量時,市民買口罩才無需提前預約,那么在整個二月份,市民無需預約即可購買口罩的天數共有多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
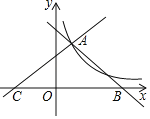
【題目】如圖直線y1=﹣x+4,y2=![]() x+b都與雙曲線y=
x+b都與雙曲線y=![]() 交于點A(1,3),這兩條直線分別與x軸交于B,C兩點.
交于點A(1,3),這兩條直線分別與x軸交于B,C兩點.
(1)求k的值;
(2)直接寫出當x>0時,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若點P在x軸上,連接AP,且AP把△ABC的面積分成1:2兩部分,則此時點P的坐標是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com