
【題目】閱讀理解:在平面直角坐標系中,若兩點P、Q的坐標分別是P(x1,y1)、
Q(x2,y2),則P、Q這兩點間的距離為|PQ|=![]() .如P(1,2),Q(3,4),則|PQ|=
.如P(1,2),Q(3,4),則|PQ|=![]() =2
=2![]() .
.
對于某種幾何圖形給出如下定義:符合一定條件的動點形成的圖形,叫做符合這個條件的點的軌跡.如平面內到線段兩個端點距離相等的點的軌跡是這條線段的垂直平分線.
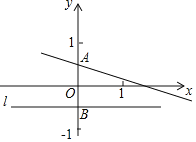
解決問題:如圖,已知在平面直角坐標系xOy中,直線y=kx+![]() 交y軸于點A,點A關于x軸的對稱點為點B,過點B作直線l平行于x軸.
交y軸于點A,點A關于x軸的對稱點為點B,過點B作直線l平行于x軸.
(1)到點A的距離等于線段AB長度的點的軌跡是 ;
(2)若動點C(x,y)滿足到直線l的距離等于線段CA的長度,求動點C軌跡的函數表達式;
問題拓展:(3)若(2)中的動點C的軌跡與直線y=kx+![]() 交于E、F兩點,分別過E、F作直線l的垂線,垂足分別是M、N,求證:①EF是△AMN外接圓的切線;②
交于E、F兩點,分別過E、F作直線l的垂線,垂足分別是M、N,求證:①EF是△AMN外接圓的切線;②![]() 為定值.
為定值.
【答案】(1)x2+(y﹣![]() )2=1;(2)動點C軌跡的函數表達式y=
)2=1;(2)動點C軌跡的函數表達式y=![]() x2;(3)①證明見解析;②證明見解析.
x2;(3)①證明見解析;②證明見解析.
【解析】
(1)利用兩點間的距離公式即可得出結論;
(2)利用兩點間的距離公式即可得出結論;
(3)①先確定出m+n=2k,mn=﹣1,再確定出M(m,﹣![]() ),N(n,﹣
),N(n,﹣![]() ),進而判斷出△AMN是直角三角形,再求出直線AQ的解析式為y=﹣
),進而判斷出△AMN是直角三角形,再求出直線AQ的解析式為y=﹣![]() x+
x+![]() ,即可得出結論;
,即可得出結論;
②先確定出a=mk+![]() ,b=nk+
,b=nk+![]() ,再求出AE=ME=a+
,再求出AE=ME=a+![]() =mk+1,AF=NF=b+
=mk+1,AF=NF=b+![]() =nk+1,即可得出結論.
=nk+1,即可得出結論.
(1)設到點A的距離等于線段AB長度的點D坐標為(x,y),
∴AD2=x2+(y﹣![]() )2,
)2,
∵直線y=kx+![]() 交y軸于點A,
交y軸于點A,
∴A(0,![]() ),
),
∵點A關于x軸的對稱點為點B,
∴B(0,﹣![]() ),
),
∴AB=1,
∵點D到點A的距離等于線段AB長度,
∴x2+(y﹣![]() )2=1,
)2=1,
故答案為:x2+(y﹣![]() )2=1;
)2=1;
(2)∵過點B作直線l平行于x軸,
∴直線l的解析式為y=﹣![]() ,
,
∵C(x,y),A(0,![]() ),
),
∴AC2=x2+(y﹣![]() )2,點C到直線l的距離為:(y+
)2,點C到直線l的距離為:(y+![]() ),
),
∵動點C(x,y)滿足到直線l的距離等于線段CA的長度,
∴x2+(y﹣![]() )2=(y+
)2=(y+![]() )2,
)2,
∴動點C軌跡的函數表達式y=![]() x2;
x2;
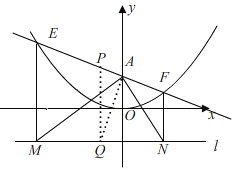
(3)①如圖,
設點E(m,a)點F(n,b),
∵動點C的軌跡與直線y=kx+![]() 交于E、F兩點,
交于E、F兩點,
∴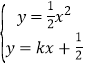 ,
,
∴x2﹣2kx﹣1=0,
∴m+n=2k,mn=﹣1,
∵過E、F作直線l的垂線,垂足分別是M、N,
∴M(m,﹣![]() ),N(n,﹣
),N(n,﹣![]() ),
),
∵A(0,![]() ),
),
∴AM2+AN2=m2+1+n2+1=m2+n2+2=(m+n)2﹣2mn+2=4k2+4,
MN2=(m﹣n)2=(m+n)2﹣4mn=4k2+4,
∴AM2+AN2=MN2,
∴△AMN是直角三角形,MN為斜邊,
取MN的中點Q,
∴點Q是△AMN的外接圓的圓心,
∴Q(k,﹣![]() ),
),
∵A(0,![]() ),
),
∴直線AQ的解析式為y=﹣![]() x+
x+![]() ,
,
∵直線EF的解析式為y=kx+![]() ,
,
∴AQ⊥EF,
∴EF是△AMN外接圓的切線;
②∵點E(m,a)點F(n,b)在直線y=kx+![]() 上,
上,
∴a=mk+![]() ,b=nk+
,b=nk+![]() ,
,
∵ME,NF,EF是△AMN的外接圓的切線,
∴AE=ME=a+![]() =mk+1,AF=NF=b+
=mk+1,AF=NF=b+![]() =nk+1,
=nk+1,
∴![]() =
=![]() =2,
=2,
即:![]() 為定值,定值為2.
為定值,定值為2.


科目:初中數學 來源: 題型:
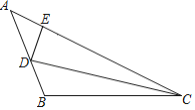
【題目】如圖,在△ABC中,∠B>90°,CD為∠ACB的角平分線,在AC邊上取點E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,則( )
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中數學 來源: 題型:
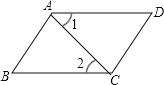
【題目】 根據題意,完成推理填空:如圖,AB∥CD,∠1=∠2,試說明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內錯角相等,兩直線平行)
∴∠BAD+∠B=180°(兩直線平行,同旁內角互補)
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數![]() ,其中
,其中![]() .
.
(1)若點![]() 在y1的圖象上.求a的值:
在y1的圖象上.求a的值:
(2)當![]() 時.若函數有最大值2.求y1的函數表達式;
時.若函數有最大值2.求y1的函數表達式;
(3)對于一次函數![]() ,其中
,其中![]() ,若對- -切實數x,
,若對- -切實數x,![]() 都成立,求a,m需滿足的數量關系及 a的取值范圍.
都成立,求a,m需滿足的數量關系及 a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
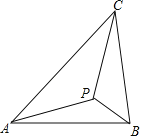
【題目】(2017湖南株洲)如圖示,若△ABC內一點P滿足∠PAC=∠PBA=∠PCB,則點P為△ABC的布洛卡點.三角形的布洛卡點(Brocard point)是法國數學家和數學教育家克洛爾(A.L.Crelle 1780﹣1855)于1816年首次發現,但他的發現并未被當時的人們所注意,1875年,布洛卡點被一個數學愛好者法國軍官布洛卡(Brocard 1845﹣1922)重新發現,并用他的名字命名.問題:已知在等腰直角三角形DEF中,∠EDF=90°,若點Q為△DEF的布洛卡點,DQ=1,則EQ+FQ=( )
A. 5 B. 4 C. 3+![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
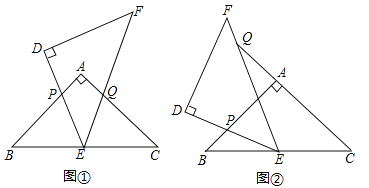
【題目】(2017甘肅省天水市)△ABC和△DEF是兩個全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的頂點E與△ABC的斜邊BC的中點重合,將△DEF繞點E旋轉,旋轉過程中,線段DE與線段AB相交于點P,線段EF與射線CA相交于點Q.
(1)如圖①,當點Q在線段AC上,且AP=AQ時,求證:△BPE≌△CQE;
(2)如圖②,當點Q在線段CA的延長線上時,求證:△BPE∽△CEQ;并求當BP=2,CQ=9時BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
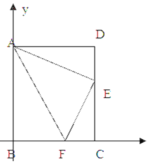
【題目】如圖,四邊形ABCD為平行四邊形紙片.把紙片ABCD折疊,使點B恰好落在CD邊上,折痕為AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求證:平行四邊形ABCD是矩形;
(2)如圖2,以點B為坐標原點,水平方向、豎直方向為x軸、y軸建立平面直角坐標系,求直線AF的解析式;
(3)在(2)中的坐標系內是否存在這樣的點P,使得以點P、A、E、F為頂點的四邊形是平行四邊形?若不存在,請說明理由;若存在,直接寫出點P的坐標。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com