
【題目】已知拋物線y=3ax2+2bx+c(a≠0)。
(1)若a=b=1,C=-1。求此拋物線與x軸的交點的坐標;
(2)若a=![]() ,c=b+2,其中b是整數。
,c=b+2,其中b是整數。
①直接寫出拋物線的頂點坐標(用含有b的代數式表示),并寫出頂點縱坐標的最大值;
②若拋物線在-2≤x≤2時,拋物線的最小值是-3,求b的值。
【答案】(1)拋物線與x軸的交點的坐標是(-1,0),(![]() ,0)
,0)
(2)①拋物線的頂點坐標(-b,-b2+b+2),最大值是2;②b=3滿足題意
【解析】分析:(1)將a、b、c的值代入,可得出拋物線解析式,從而可求解拋物線與x軸的交點坐標;(2)a=![]() ,c-b=2,則拋物線可化為y=
,c-b=2,則拋物線可化為y=![]() +2bx+b+2,其對稱軸為x= -b,分x= -b<-1,x= - b>2兩種情況討論b的取值,根據最小值為-3,可得出方程,求出b的值即可.
+2bx+b+2,其對稱軸為x= -b,分x= -b<-1,x= - b>2兩種情況討論b的取值,根據最小值為-3,可得出方程,求出b的值即可.
本題解析:(1)因為a=b=1,c=-1,所以拋物線解析式y=3x2+2x-1
令y=0,得3x2+2x-1=0解得x1=-1,x2=![]()
所以此時拋物線與x軸的交點的坐標是(-1,0),(![]() ,0)。
,0)。
(2)若a=![]() ,c=b+2,其中b是整數,拋物線解析式y=x2+2bx+b+2=(x+b)2-b2+b+2
,c=b+2,其中b是整數,拋物線解析式y=x2+2bx+b+2=(x+b)2-b2+b+2
①拋物線的頂點坐標(-b,-b2+b+2),所以頂點縱坐標的最大值是2.
②a=![]() ,c=b+2,則拋物線可化為y=
,c=b+2,則拋物線可化為y=![]() +2bx+b+2,其對稱軸為x=b,
+2bx+b+2,其對稱軸為x=b,
當x=b<2時,即b>2,則有拋物線在x=2時取最小值為3,
此時3=![]() +2×(2)b+b+2,
+2×(2)b+b+2,
解得:b=3,符合題意;
當x=b>2時,即b<2,則有拋物線在x=2時取最小值為3,
此時3=![]() +2×2b+b+2,
+2×2b+b+2,
解得:b=![]() ,不合題意,舍去,
,不合題意,舍去,
當1≤b≤2時,即2≤b≤1,則有拋物線在x=b時取最小值為3,
此時3=![]() +2×(b)b+b+2,
+2×(b)b+b+2,
化簡得: ![]() b5=0,
b5=0,
解得:b=![]() (不合題意,舍去),b=
(不合題意,舍去),b=![]() ,
,
綜上可得:b=3或b=![]() .
.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與正比例函數y=2x的圖象交于點A(m,2),與y軸的交點為C,與x軸的交點為D. 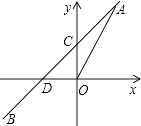
(1)m=;
(2)若一次函數圖象經過點B(﹣2,﹣1),求一次函數的解析式;
(3)在(2)的條件下,求△AOD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了提升初中學生學習數學的興趣,培養學生的創新精神,舉辦了“玩轉數學”比賽.評委從研究報告、小組展示、答辯三個方面為每個參賽小組打分,按照研究報告占40%,小組展示占30%,答辯占30%計算各小組的成績,各項成績均按百分制記錄.甲小組的研究報告得85分,小組展示得90分,答辯得80分,則甲小組的參賽成績為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線交⊙O于點D,過點D作DE⊥AC交AC的延長線于點E,連接BD。

(1)求證:DE是⊙O的切線;
(2)若tan∠ABD=2,CE=1,求⊙O的半徑。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【探索新知】
己知平面上有![]() (
(![]() 為大于或等于
為大于或等于![]() 的正整數)個點
的正整數)個點![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,從第
,從第![]() 個點
個點![]() 開始沿直線滑動到另一個點,且同時滿足以下三個條件:①每次滑動的距離都盡可能最大;②
開始沿直線滑動到另一個點,且同時滿足以下三個條件:①每次滑動的距離都盡可能最大;②![]() 次滑動將每個點全部到達一次;③滑動
次滑動將每個點全部到達一次;③滑動![]() 次后必須回到第
次后必須回到第![]() 個點
個點![]() ,我們稱此滑動為“完美運動”,且稱所有點為“完美運動”的滑動點,記完成
,我們稱此滑動為“完美運動”,且稱所有點為“完美運動”的滑動點,記完成![]() 個點的“完美運動”的路程之和為
個點的“完美運動”的路程之和為![]() .
.
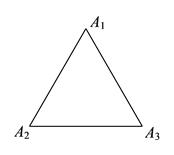
(![]() )如圖
)如圖![]() ,滑動點是邊長為
,滑動點是邊長為![]() 的等邊三角形的三個頂點,此時
的等邊三角形的三個頂點,此時![]() =__________.
=__________.
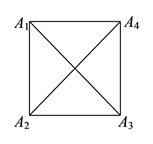
(![]() )如圖
)如圖![]() ,滑動點是邊長為
,滑動點是邊長為![]() 、對角線(線段
、對角線(線段![]() 、
、![]() )長為
)長為![]() 的正方形四個頂點,此時
的正方形四個頂點,此時![]() __________.
__________.
【深入研究】
現有![]() 個點恰好在同一直線上,相鄰兩點間距離都為
個點恰好在同一直線上,相鄰兩點間距離都為![]() .
.
(![]() )如圖
)如圖![]() ,當
,當![]() 時,直線上的點分別為點
時,直線上的點分別為點![]() 、
、![]() 、
、![]() .
.
![]()
為了完成“完美運動”,滑動的步驟給出如圖![]() 所示的兩種方法:
所示的兩種方法:


方法![]() :
: ![]() , 方法
, 方法![]() :
: ![]()
①其中正確的方法為( ).
A.方法![]() B.方法
B.方法![]() C.方法
C.方法![]() 和方法
和方法![]()
②完成此“完美運動”的![]() __________.
__________.
(![]() )當
)當![]() 分別取
分別取![]() 、
、![]() 時,對應的
時,對應的![]() __________,
__________, ![]() __________.
__________.
(![]() )若直線上有
)若直線上有![]() 個點,請用含
個點,請用含![]() 的代教式表示
的代教式表示![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-6mx+9m2-9=0。
(1)求證:此方程有兩個不相等的實數根;
(2)設此方程的兩個根分別為x1、x2。若2x1=x2-3,求m的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某一時刻,身高1.6m的小明在陽光下的影長是0.4m.同一時刻同一地點,測得某旗桿的影長是5m,則該旗桿的高度是 ( )
A.1.25mB.10mC.20mD.8m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com