若關于x的方程k(x2-4)+ax-1=0對一切實數k都有實數根,求a的取值范圍.
解:∵關于x的方程k(x
2-4)+ax-1=0,
∴kx
2+ax-4k-1=0,
①當k=0時,方程為ax-4k-1=0,
∵方程對一切實數k都有實數根,
∴a≠0;
②當k≠0時,方程為一元二次方程,
∵方程對一切實數k都有實數根,
∴方程的判別式是非負數,
即△=a
2+4k(4k+1)=a
2+16k
2+4k,
由一元二次方程有根的條件可得:a
2+4k(4k+1)≥0時方程有實數解,
(1)當k>0時,上式必定成立,此時a可取任意值;
(2)當k<0時,上式a
2+4k(4k+1)≥0中,a
2≥0,4k<0,考慮4k+1的正負性:
A:若4k+1>0,即:-

<k<0,
∴0<4k(4k+1)<1,
此時a可取任意值;
B:若4k+1<0,
即:k<-

,
∴4k(4k+1)>0,
此時a可取任意值;
C:若4k+1=0,
即:k=-

,
∴4k(4k+1)=1,
此時a可取任意值;
綜上所述:只要a的值不為0即可.
分析:首先把方程整理為kx
2+ax-4k-1=0,然后討論:
①當k=0時,方程為ax-4k-1=0,由于方程對一切實數k都有實數根,所以根據一元一次方程的定義即可求出a的取值范圍;
②當k≠0時,方程為一元二次方程,由于方程對一切實數k都有實數根,所以得到方程的判別式是非負數,由此即可求出a的取值范圍.
點評:此題主要考查了一元二次方程的判別式和方程的根的關系,也利用了分類討論的思想,題目對于學生分析問題、解決問題的能力要求比較高,平時應該加強這方面的訓練.

 <k<0,
<k<0, ,
, ,
,

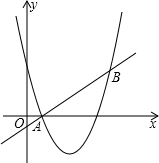 直線y=x+a和拋物線y=x2+bx+c都經過A(1,0)、B(3,2)兩點,且不等式x+a>x2+bx+c 的整數解為K,若關于x的方程x2-(m2+5)x+2m2+6=0的兩實根之差的絕對值為n,且n滿足n=2(K+1),求m的值.
直線y=x+a和拋物線y=x2+bx+c都經過A(1,0)、B(3,2)兩點,且不等式x+a>x2+bx+c 的整數解為K,若關于x的方程x2-(m2+5)x+2m2+6=0的兩實根之差的絕對值為n,且n滿足n=2(K+1),求m的值.